
【题目】某公司到果园基地购买某种水果慰问医务工作者,果园基地向购买超过![]() 以上(含
以上(含![]() )的客户推出两种购买方式.方式甲:价格为
)的客户推出两种购买方式.方式甲:价格为![]() 元
元![]() ,由果园基地运送到公司;方式乙:价格为
,由果园基地运送到公司;方式乙:价格为![]() 元
元![]() ,由顾客自己租车运回,从果园基地到公司的租车费用为
,由顾客自己租车运回,从果园基地到公司的租车费用为![]() 元.设该公司购买水果的数量为
元.设该公司购买水果的数量为![]() (
(![]() ).
).
(1)根据题意,填写下表:
购买水果的数量(kg) |
|
|
| … |
方式甲的总费用(元) |
| … | ||
方式乙的总费用(元) |
| … |
(2)设该公司按方式甲购买水果的总费用为![]() 元,按方式乙购买水果的总费用为
元,按方式乙购买水果的总费用为![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
① 若按方式甲购买水果的总费用和按方式乙购买水果的总费用相同,则该公司购买水果的数量为 ![]() ;
;
② 若该公司购买水果的数量为![]() ,则按方式甲、方式乙中的方式 购买水果的总费用少;
,则按方式甲、方式乙中的方式 购买水果的总费用少;
③ 若该公司购买水果的总费用为![]() 元,则按方式甲、方式乙中的方式 购买水果的数量多.
元,则按方式甲、方式乙中的方式 购买水果的数量多.
【答案】(1)见解析;(2)![]() ,
,![]() ;
;![]() ,
,![]() ;(3)①5000;②乙;③甲
;(3)①5000;②乙;③甲
【解析】
(1)根据甲乙两种购买方式可以算出当购买水果的数量分别为3500、5500千克时所需的费用;
(2)方式甲费用为:9×水果数量;方式乙费用为:8×水果数量+5000,注意自变量的取值均为不小于3000;
(3)①令![]() ,求出x即可;
,求出x即可;
②令x=5200,分别代入,比较![]() 和
和![]() 的大小即可;
的大小即可;
③分别令![]() 和
和![]() 的值为39000,解出x,再比较大小即可.
的值为39000,解出x,再比较大小即可.
解:(1)由题意可得:
当购买水果的数量为3500千克时,
方式甲的总费用=3500×9=31500元,
方式乙的总费用=3500×8+5000=33000元,
当购买水果的数量为5500千克时,
方式甲的总费用=5500×9=49500元,
方式乙的总费用=5500×8+5000=49000元,
故填表如下:
购买水果的数量(kg) |
|
|
| … |
方式甲的总费用(元) | 31500 |
| 49500 | … |
方式乙的总费用(元) | 33000 |
| 49000 | … |
(2)根据题意得:
![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
(3)① 令![]() ,即9x=8x+5000,
,即9x=8x+5000,
解得:x=5000,
故答案为:5000;
② 若该公司购买水果的数量为![]() kg,
kg,
则方式甲所需费用=9×5200=46800元,
方式乙所需费用=8×5200+5000=46600元,
46800>46600,
∴方式乙购买水果的总费用少;
③令![]() ,即9x=39000,
,即9x=39000,
解得:x=![]() ,
,
令![]() ,即8x+5000=39000,
,即8x+5000=39000,
解得:x=4250,
![]() >4250,
>4250,
∴方式甲购买水果的数量多.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校举行“经典诵读”比赛,诵读材料有:A《唐诗》、B《宋词》、C《论语》.将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小红和小亮参加诵读比赛,比赛时小红先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行比赛.
(1)小红诵读《论语》的概率是 ;
(2)请用列表法或画树状图的方法,求小红和小亮诵读两个相同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点![]() 的横、纵坐标的绝对值之和叫做点
的横、纵坐标的绝对值之和叫做点![]() 的勾股值,记
的勾股值,记![]()
![]() .若抛物线
.若抛物线![]() 与直线
与直线![]() 只有一个交点
只有一个交点![]() ,已知点
,已知点![]() 在第一象限,且
在第一象限,且![]() ,令
,令![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的四个顶点坐标分别是
的四个顶点坐标分别是![]() 、
、![]() 、
、![]() 、
、![]() .函数
.函数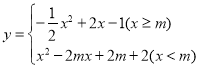 (
(![]() 为常数).
为常数).
(1)当此函数的图象经过点![]() 时,求此函数的表达式;
时,求此函数的表达式;
(2)在(1)的条件下,当![]() 时,求函数值
时,求函数值![]() 的取范围;
的取范围;
(3)当此函数的图象与矩形![]() 的边有两个交点时,直接出
的边有两个交点时,直接出![]() 的取值范围;
的取值范围;
(4)记此函数在![]() 范围内的纵坐标为
范围内的纵坐标为![]() ,若存在
,若存在![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
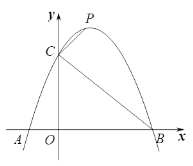
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某印刷厂每五年需淘汰一批同款的旧打印机并购买新机.购买新机时,若同时配买墨盒,每盒![]() 元,且最多可配买
元,且最多可配买![]() 盒;若非同时配买,则每盒需
盒;若非同时配买,则每盒需![]() 元.根据该厂以往的记录,
元.根据该厂以往的记录,![]() 台同款打印机正常工作五年消耗的墨盒数如下表:
台同款打印机正常工作五年消耗的墨盒数如下表:

(1)以这![]() 台打印机五年消耗的墨盒数为样本,估计“一台该款打印机正常工作五年消耗的墨盒数不大于
台打印机五年消耗的墨盒数为样本,估计“一台该款打印机正常工作五年消耗的墨盒数不大于![]() ”的概率;
”的概率;
(2)如果每台打印机购买新机时配买的墨盒只能供本机使用,试以这![]() 台打印机消耗墨盒费用的平均数作为决策依据,说明购买
台打印机消耗墨盒费用的平均数作为决策依据,说明购买![]() 台该款打印机时,应同时配买
台该款打印机时,应同时配买![]() 盒还是
盒还是![]() 盒墨?
盒墨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]()
![]() 经过原点和点
经过原点和点![]() ,顶点为
,顶点为![]() ,抛物线
,抛物线![]() 与抛物线
与抛物线![]() 关于原点
关于原点![]() 对称.
对称.
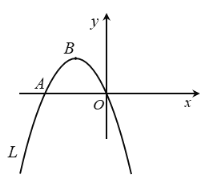
(1)求抛物线![]() 的函数表达式及点
的函数表达式及点![]() 的坐标;
的坐标;
(2)已知点![]() 、
、![]() 在抛物线
在抛物线![]() 上的对应点分别为
上的对应点分别为![]() 、
、![]() ,
,![]() 的对称轴交
的对称轴交![]() 轴于点
轴于点![]() ,则抛物线
,则抛物线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“普洱茶”是云南有名的特产,某网店专门销售某种品牌的普洱茶,成本为30元/盒,每天销售![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天该种普洱茶的销售量不低于240盒,该网店店主热心公益事业,决定从每天的销售利润中捐出500元给扶贫基金会,当销售单价为多少元时,每天获取的净利润最大,最大净利润是多少?(注:净利润=总利润-捐款)
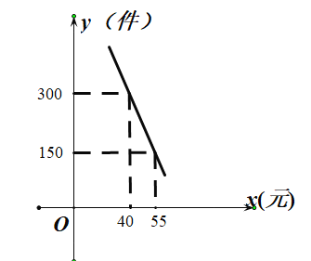
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com