
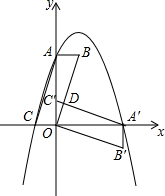
 ��ƽ��ֱ������ϵ�У�?ABOC��ͼ���ã���C�������ǣ�-1��0������A��y����������ϣ�����ƽ���ı����Ƶ�O˳ʱ����ת90�㣬��?A��B��OC�䣬������y=ax2+bx+4����C��A��A�䣬��M�Ǵ������ߵ�һ���㣬���M�ĺ�����Ϊm��
��ƽ��ֱ������ϵ�У�?ABOC��ͼ���ã���C�������ǣ�-1��0������A��y����������ϣ�����ƽ���ı����Ƶ�O˳ʱ����ת90�㣬��?A��B��OC�䣬������y=ax2+bx+4����C��A��A�䣬��M�Ǵ������ߵ�һ���㣬���M�ĺ�����Ϊm������ ��1�����C��-1��0����A�䣨4��0������y=ax2+bx+4��ת��Ϊ�����������⣮
��2����ͼ1�У����������ٵ���M��y���ұ�ʱ����M��m��-m2+3m+4��������S=S��AMO+S��OMA��-S��AOA�����㼴�ɣ��ڵ���M��y������ʱ����M1��m��-m2+3m+4��������S=${S}_{��AO{M}_{1}}$+S��AOA��-${S}_{��A��O{M}_{1}}$���㼴�ɣ�
��3�����ݣ�2���еķֶκ������ֱ����S��ȡֵ��Χ�������жϣ�
��4���������������ۢ��Ե�M��N��B��QΪ������ı��������ĶԳ�ͼ�Σ���BQΪ��ʱ������BQN1M1������BQN2M2�����ĶԳ�ͼ�Σ����Ե�M��N��B��QΪ������ı��������ĶԳ�ͼ�Σ���BQΪ�Խ���ʱ��ƽ���ı���BM1QN3�����ĶԳ�ͼ�Σ�
��5�����ã�4���еĽ��ۼ��ɵó����ۣ�
��� �⣺��1��������A��0��4����C��-1��0����A�䣨4��0����
��C��-1��0����A�䣨4��0������y=ax2+bx+4��$\left\{\begin{array}{l}{a-b+4=0}\\{16a+4b+4=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$��
�������ߵĽ���ʽy=-x2+3x+4��
��2����ͼ1�У�
�ٵ���M��y���ұ�ʱ����M��m��-m2+3m+4����
S=S��AMO+S��OMA��-S��AOA��=$\frac{1}{2}$•4•m+$\frac{1}{2}$•4•��-m2+3m+4��-$\frac{1}{2}$•4•4=-2m2+8m��
�ڵ���M��y������ʱ����M1��m��-m2+3m+4����
S=${S}_{��AO{M}_{1}}$+S��AOA��-${S}_{��A��O{M}_{1}}$=$\frac{1}{2}$•4•��-m��+$\frac{1}{2}$•4•4-$\frac{1}{2}$•4•��-m2+3m+4��=2m2-8m��
����������S=$\left\{\begin{array}{l}{2{m}^{2}-8m}&{��-1��m��0��}\\{-2{m}^{2}+8m}&{��0��m��4��}\end{array}\right.$��
��3���ɣ�2����֪����-1��m��0ʱ��0��s��10��
��0��m��-4ʱ��0��S��8��
�൱m=-1ʱ��S��ֵ������ֵΪ10����ʱM��-1��0����
��4����ͼ2�У�
���Ե�M��N��B��QΪ������ı��������ĶԳ�ͼ�Σ���BQΪ��ʱ������BQN1M1������BQN2M2�����ĶԳ�ͼ�Σ���ʱN1��3��0����N2��0��0����
���Ե�M��N��B��QΪ������ı��������ĶԳ�ͼ�Σ���BQΪ�Խ���ʱ��ƽ���ı���BM1QN3�����ĶԳ�ͼ�Σ���ʱN3��-1��0����
������������M��N��B��QΪ������ı��������ĶԳ�ͼ�Σ�tֵΪ-1��0��3��
��5���ɣ�4����֪���Ե�M��N��B��QΪ������ı��μ������ĶԳ�ͼ�Σ�������Գ�ͼ��ʱ��tֵΪ0��3��
���� ���⿼����κ����ۺ��⡢����ϵ�����������ε���������ĶԳ�ͼ�Ρ���Գ�ͼ�ε�֪ʶ������Ĺؼ����������⣬ѧ���÷������۵�˼��˼�����⣬��������Ҫȫ�棬ע�ⲻ��©�⣬�����п�ѹ���⣮


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪AE��BD�ǡ�ABC�Ľ�ƽ���ߣ�AE��BD�ཻ�ڵ�P����AB=BC����AB��AC����ͼ�е�ȫ���������У�������
��ͼ����֪AE��BD�ǡ�ABC�Ľ�ƽ���ߣ�AE��BD�ཻ�ڵ�P����AB=BC����AB��AC����ͼ�е�ȫ���������У�������| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��y=x-3��x�ᡢy��ֱ��ཻ�ڵ�A��B������A��B�����������y=-x2+bx+c��x�����һ������ΪC��
��ͼ��ֱ��y=x-3��x�ᡢy��ֱ��ཻ�ڵ�A��B������A��B�����������y=-x2+bx+c��x�����һ������ΪC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ƽ���� | B�� | �� | C�� | ���� | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20�� | B�� | 40���140�� | C�� | 40�� | D�� | 20���160�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com