
【题目】阅读材料:
某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如,图①可以解释![]() ,因此,我们可以利用这种方法对某些多项式进行因式分解.
,因此,我们可以利用这种方法对某些多项式进行因式分解.
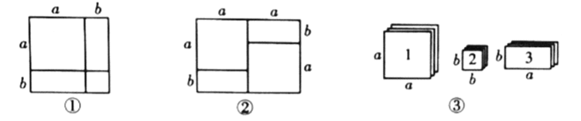
根据阅读材料回答下列问题:
(1)如图②所表示的因式分解的恒等式是________________________.
(2)现有足够多的正方形和长方形卡片(如图③),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形(每两张卡片之间既不重叠,也无空隙),使该长方形的面积为![]() ,并利用你画的长方形的面积对
,并利用你画的长方形的面积对![]() 进行因式分解.
进行因式分解.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列条件:①∠A+∠B=∠C,②∠C=90°,③AC:BC:AB=3:4:5,④∠A:∠B:∠C=3:4:5.⑤a2=(b+c)(b﹣c)中,能确定△ABC是直角三角形的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
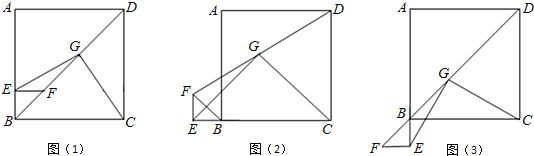
【题目】在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连结EG、CG.
(1)如图1,求证EG=CG且EG⊥CG.
(2)如图2将△BEF绕点B逆时针旋转90度,求线段EG和CG有怎么样的关系,并证明你的结论.
(3)如图3,将△BEF绕点B逆时针旋转180度,线段EG和CG有怎么样的关系?写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
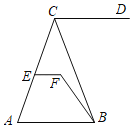
【题目】如图,EF∥AB,∠DCB=65°,∠CBF=15°,∠EFB=130°.
(1)直线CD与AB平行吗?为什么?
(2)若∠CEF=68°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
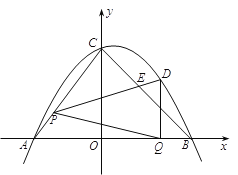
【题目】如图,在平面直角坐标系![]() 中,已知A(-3,0),B(4,0),C(0,4). 二次函数的图像经过A、B、C三点.点P沿AC由点A处向点C运动,同时,点Q沿BO由点B处向点O运动,运动速度均为每秒1个单位长度.当一个点停止运动时,另一个点也随之停止运动.连接PQ,过点Q作QD⊥x轴,与二次函数的图像交于点D,连接PD,PD与BC交于点E. 设点P的运动时间为t秒(t>0).
中,已知A(-3,0),B(4,0),C(0,4). 二次函数的图像经过A、B、C三点.点P沿AC由点A处向点C运动,同时,点Q沿BO由点B处向点O运动,运动速度均为每秒1个单位长度.当一个点停止运动时,另一个点也随之停止运动.连接PQ,过点Q作QD⊥x轴,与二次函数的图像交于点D,连接PD,PD与BC交于点E. 设点P的运动时间为t秒(t>0).
⑴ 求二次函数的表达式;
⑵ 在点P、Q运动的过程中,当∠PQA+∠PDQ=90°时,求t的值;
⑶ 连接PB、BD、CD,试探究在点P,Q运动的过程中,是否存在某一时刻,使得四边形PBDC是平行四边形?若存在,请求出此时t的值与点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某动物园在![]() 天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 (单位:万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若![]() 月
月![]() 日的游客人数记为
日的游客人数记为![]() 万人,请用含
万人,请用含![]() 的代数式表示
的代数式表示![]() 月
月![]() 日的游客人数,并直接写出七天内游客人数最多的是哪一天?
日的游客人数,并直接写出七天内游客人数最多的是哪一天?
(2)若![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,门票每人
万人,门票每人![]() 元,问黄金周期间该动物园门票总收入是多少万元?
元,问黄金周期间该动物园门票总收入是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:

我们把表格中字母的和所得的多项式称为"'特征多项式",例如:第1格的“特征多项式”为 4x+y,第 2 格的“特征多项式”为 8x+4y, 回答下列问题:
(1)第 3 格的“特征多项式”为 第 4 格的“待征多项式”为 , 第 n 格的“特征多项式”为 .
(2)若第 m 格的“特征多项式”与多项式-24x+2y-5 的和不含有 x 项,求此“特征多项式”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com