
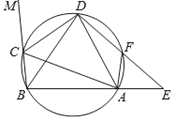
【题目】如图,在圆内接四边形ABCD中,CD为△BAC的外角平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.
(1)求证:AD=BD;
(2)若AC=10,AF=3,DF:FE=3:2,求DE的长.
【答案】(1)证明见解析;(2)5![]() .
.
【解析】
(1)由圆内接四边形的性质以及圆的性质可求得∠DBA=∠DAB,从而证明AD=BD;
(2)由条件可证得△AEF∽△DAC,再利用相似三角形的性质可求得DE的长.
(1)证明:∵CD平分∠ACM,∴∠ACD=∠MCD,
∵四边形ABCD为圆内接四边形,∴∠MCD=∠BAD,
又∠ACD=∠ABD,∴∠BAD=∠ABD,∴AD=BD;
(2)解:∵BD=AD,BC=AF,∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,∴CD=DF,∵BC=AF,∴∠BDC=∠ADF,∴∠CDA=∠BDF=∠EAF,
,∴CD=DF,∵BC=AF,∴∠BDC=∠ADF,∴∠CDA=∠BDF=∠EAF,
由(1)可知∠DCA=∠DBA,且∠EFA=∠DBA,
∴∠DCA=∠EFA,∴△AEF∽△DAC,∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() ,∴EFDF=30,∵DF:FE=3:2,
,∴EFDF=30,∵DF:FE=3:2,
∴设DF=3x,则FE=2x,∴6x2=30,解得x=![]() ,
,
∴DE=DF+FE=5x=5![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,等边三角形 ABC 的边长为 3,过点 B 的直线 l⊥AB,且△ABC 与△A′BC′关于直线 l 对称,D 为线段 BC′上一动点,则 AD+CD 的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角ΔABC中,已知AB=AC,D为底边BC上的一点,E为线段AD上的一点,且∠BED=∠BAC=2∠DEC,连接CE.
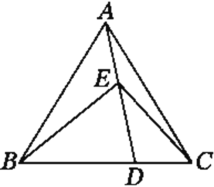
(1)求证:∠ABE=∠DAC
(2)若∠BAC=60°,试判断BD与CD有怎样的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
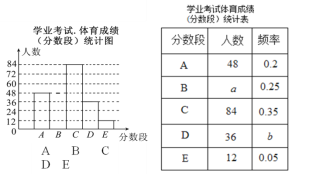
【题目】为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分;B:49~45分;C:44~40分;D:39~30分;E:29~0分)统计如下:根据上面提供的信息,回答下列问题:
(1)a的值为_ _,b的值为 _ _,并将统计图补充完整.
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”甲同学的体育成绩应在什么分数段内?
(3)若成绩在40分以上(含40分))为优秀,估计该市今年10440名九年级学生中体育成绩为优秀的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,M(m,n)且m、n满足m2+2n2﹣2mn+4n+4=0,B(0,b)为y轴上一动点,绕B点将直线BM顺时针旋转45°交x轴于点C,过C作AC⊥BC交直线BM于点A(a,t).

(1)求点M的坐标;
(2)如图1,在B点运动的过程中,A点的横坐标是否会发生变化?若不变,求a的值;若变化,写出A点的横坐标a的取值范围;
(3)如图2,过T(a,0)作TH⊥BM(垂足H在x轴下方),在射线HB上截取HK=HT,连OK,求∠OKB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑销售商试销某一品牌电脑(出厂为![]() 元/台)以
元/台)以![]() 元/台销售时,平均每月可销售
元/台销售时,平均每月可销售![]() 台,现为了扩大销售,销售商决定降价销售,在原来
台,现为了扩大销售,销售商决定降价销售,在原来![]() 月份平均销售量的基础上,经
月份平均销售量的基础上,经![]() 月份的市场调查,
月份的市场调查,![]() 月份调整价格后,月销售额达到
月份调整价格后,月销售额达到![]() 元.已知电脑价格每台下降
元.已知电脑价格每台下降![]() 元,月销售量将上升
元,月销售量将上升![]() 台.
台.
![]() 求
求![]() 月份到
月份到![]() 月份销售额的月平均增长率;
月份销售额的月平均增长率;
![]() 求
求![]() 月份时该电脑的销售价格.
月份时该电脑的销售价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
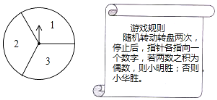
【题目】如图可以自由转动的转盘被![]() 等分,指针落在每个扇形内的机会均等.
等分,指针落在每个扇形内的机会均等.
![]() 现随机转动转盘一次,停止后,指针指向数字
现随机转动转盘一次,停止后,指针指向数字![]() 的概率为________;
的概率为________;
![]() 小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com