
【题目】如图,两个全等的Rt△AOB、Rt△OCD分别位于第二、第一象限,∠ABO=∠ODC=90°,OB、OD在x轴上,且∠AOB=30°,AB=1.
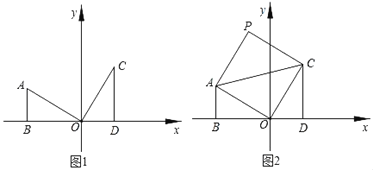
(1)如图1中Rt△OCD可以看作由Rt△AOB先绕点O顺时针旋转 度,再绕斜边中点旋转 度得到的,C点的坐标是 ;
(2)是否存在点E,使得以C、O、D、E为顶点的四边形是平行四边形,若存在,写出E点的坐标;若不存在请说明理由.
(3)如图2将△AOC沿AC翻折,O点的对应点落在P点处,求P点的坐标.
【答案】(1)90,180,(1,![]() );(2)存在,E的坐标为(0,
);(2)存在,E的坐标为(0,![]() )或(2,
)或(2,![]() ),或(0,﹣
),或(0,﹣![]() );(3)P(1﹣
);(3)P(1﹣![]() ,1+
,1+![]() ).
).
【解析】
(1)先求出OB,再由旋转求出OD,CD,即可得出结论;
(2)先求出D的坐标,再分三种情况,利用平行四边形的性质即可得出结论;
(3)先判断出四边形OAPC是正方形,再利用中点坐标公式即可得出结论
解:(1)Rt△OCD可以看作由Rt△AOB先绕点O顺时针旋转90°,再绕斜边中点旋转180°得到的,
在Rt△AOB中,∠AOB=30°,AB=1,
∴OB=![]() ,
,
由旋转知,OD=AB=1,CD=OB=![]() ,
,
∴C(1,![]() ),
),
故答案为90,180,(1,![]() );
);
(2)存在,理由:如图1,
由(1)知,C(1,![]() ),
),
∴D(1,0),
∵O(0,0),
∵以C、O、D、E为顶点的四边形是平行四边形,
∴①当OC为对角线时,
∴CE∥OD,CE=OD=1,点E和点B'重合,
∴E(0,![]() ),
),
②当CD为对角线时,CE∥OD,CE=OD=1,
∴E(2,![]() ),
),
当OD为对角线时,OE'∥CD,OE'=CD![]() ,
,
∴E(0,﹣![]() ),
),
即:满足条件的E的坐标为(0,![]() )或(2,
)或(2,![]() ),或(0,﹣
),或(0,﹣![]() );
);
(3)由旋转知,OA=OC,∠OCD=∠AOB=30°,
∴∠COD=90°﹣∠OCD=60°,
∴∠AOC=90°,
由折叠知,AP=OA,PC=OC,
∴四边形OAPC是正方形,
设P(m,n)
∵A(﹣![]() ,1),C(1,
,1),C(1,![]() ),O(0,0),
),O(0,0),
∴![]() (m+0)=
(m+0)=![]() (1﹣
(1﹣![]() ),
),![]() (n+0)=
(n+0)=![]() (1+
(1+![]() ),
),
∴m=1﹣![]() ,n=1+
,n=1+![]() ,
,
∴P(1﹣![]() ,1+
,1+![]() ).
).


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
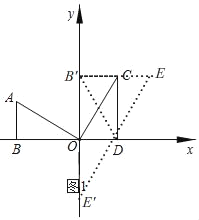
【题目】如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM运动,当他运动2米到达点D处时,测得影长DN=0.6 m,再前进2米到达点B处时,测得影长MB=1.6 m.(图中线段AB、CD、EF表示小明的身高)
(1)请画出路灯O的位置和小明位于F处时,在路灯灯光下的影子;
(2)求小明位于F处的影长.
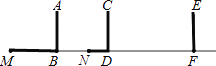
查看答案和解析>>
科目:初中数学 来源: 题型:
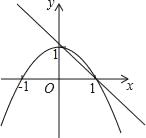
【题目】如图,已知抛物线y1=﹣x2+1,直线y2=﹣x+1,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=2时,y1=﹣3,y2=﹣1,y1<y2,此时M=﹣3.下列判断中:
①当x<0或x>1时,y1<y2;
②当x<0时,M=y1;
③使得M=![]() 的x的值是﹣
的x的值是﹣![]() 或
或![]() ;
;
④对任意x的值,式子![]() =1﹣M总成立.
=1﹣M总成立.
其中正确的是_____(填上所有正确的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
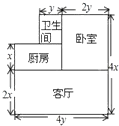
【题目】小李家住房结构如图所示,小李打算把卧室和客厅铺上木地板.
(1)请问他至少需要买多少平方米的木地板?(用字母表示)
(2)若![]() 米,
米,![]() 米时,并且每平方米木地板的价格是
米时,并且每平方米木地板的价格是![]() 元,则他至少需要准备多少元钱?
元,则他至少需要准备多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
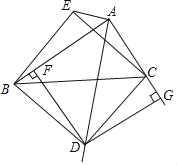
【题目】如图,含45°角的直角三角板DBC的直角顶点D在∠BAC的角平分线AD上,DF⊥AB于F,DG⊥AC于G,将△DBC沿BC翻转,D的对应点落在E点处,当∠BAC=90°,AB=4,AC=3时,△ACE的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.
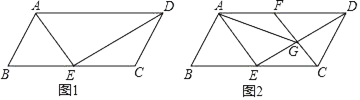
(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离![]() (千米)和行驶时间t(小时)之间的函数关系图象如图所示. 根据题目和图象提供的信息,下列说法正确的是( )
(千米)和行驶时间t(小时)之间的函数关系图象如图所示. 根据题目和图象提供的信息,下列说法正确的是( )
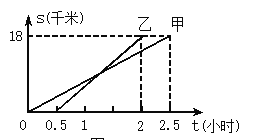
A. 乙比甲早出发半小时 B. 乙在行驶过程中没有追上甲
C. 乙比甲先到达B地 D. 甲的行驶速度比乙的行驶速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC=4cm,将△ABC沿CA方向平移4cm得到△EFA,连接BE,BF;BE与AF交于点G
(1)判断BE与AF的位置关系,并说明理由;
(2)若∠BEC=15°,求四边形BCEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
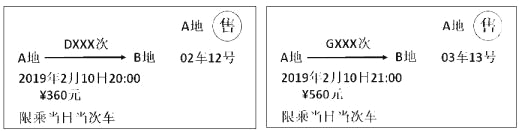
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com