
����Ŀ���������Һ������ۺ�������������ʽ����������ij��̣����ɼס����������Ӻ�����6���¿�����ɣ����ɼס������Ӷ������ӱ��Ҷ�����5���µ�ʱ����ɣ�
��1���ס������ӵ����������̸��輸���µ�ʱ�䣿
��2����֪��ÿ��ʩ������Ϊ15��Ԫ�����ҶӶ�6��Ԫ����Ҫ��ù����ܷ��ò�����141��Ԫ�����̱�����һ���ڿ���������12���£���Ϊ��ȷ�����Ѻ��ڣ���ȡ����a���£��Ҷ���b���£�a��b��Ϊ�������ֹ������ķ�ʽʩ���������ļ���ʩ��������
���𰸡���1������Ҫ10������ɣ��Ҷ���Ҫ15������ɣ�2����2��ʩ������������2���£��Ҷ���12���£�����4���£��Ҷ���9����
��������
��1�����Ҷ���Ҫx������ɣ������Ҫ��x��5��������ɣ��������Ӻ���6����������x��ֵ���ɣ�
��2�����ݷ��ò�����141��Ԫ�г�һԪһ�β���ʽ��⼴��
�⣺��1�����Ҷ���Ҫx������ɣ������Ҫ��x��5��������ɣ�
��������ã�![]() ����ã�x=15��
����ã�x=15��
������x=15��ԭ���̵ĸ���
��x=15ʱ��x��5=10��
�𣺼���Ҫ10������ɣ��Ҷ���Ҫ15������ɣ�
��2����������ã�15a+9b��141��![]() ��
��
��ã�a��4��b��9��
��a��b������������a=2��b=12��a=4��b=9��
����2��ʩ������������2���£��Ҷ���12���£�����4���£��Ҷ���9���£�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=9��AC=6��BC=12����M��AB���ϣ���AM=3������M��ֱ��MN��AC�߽��ڵ�N��ʹ�صõ���������ԭ���������ƣ���MN=__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ��һ�β����н��������:����x2=a2,��x=a;�ڷ���2x(x-1)-x+1=0�Ľ���x=1;����֪���������߷ֱ�Ϊ2��9,�����߳��Ƿ���x2-14x+48=0�ĸ�,����������ε��ܳ���17��19.���д���ȫ��ȷ����Ŀ������(����)
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��![]() ����������ʾ�����˶���ÿ������������OABC�ı�ʱ����з���������ʱ����ǵ�������ǣ�����P��2018�����������εı�ʱ����P������Ϊ______��
����������ʾ�����˶���ÿ������������OABC�ı�ʱ����з���������ʱ����ǵ�������ǣ�����P��2018�����������εı�ʱ����P������Ϊ______��

���𰸡�![]()
��������
���ݷ����������ǵĶ�������ͼ�Σ���ͼ��֪��ÿ6�η���Ϊһ��ѭ��������ѭ������2018����6�������̺����������ȷ������Ӧ�ĵ�����꼴�ɣ�
�⣺��ͼ��ʾ������6�η�����ص�������![]() ��
��
![]() ��
��
![]() ����P��2018���������εı�ʱΪ��337��ѭ����ĵ�2�η�����
����P��2018���������εı�ʱΪ��337��ѭ����ĵ�2�η�����
![]() ��P������Ϊ
��P������Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
���㾦��
������Ҫ�����˵������Ĺ��ɣ�����ͼ�Σ��۲��ÿ6�η���Ϊһ��ѭ��������ѭ���ǽ���Ĺؼ���
�����͡������
��������
15
����Ŀ��Ϊ�˱���������ij������˾��������A��B�����ͺŵ�ȫ�»�϶�����������10��������A���ͺ�ÿ���۸�Ϊa��Ԫ��ÿ���ʡ����Ϊ![]() ������B���ͺ�ÿ���۸�Ϊb��Ԫ��ÿ���ʡ����Ϊ
������B���ͺ�ÿ���۸�Ϊb��Ԫ��ÿ���ʡ����Ϊ![]() �����������飬����һ��A�ͳ��ȹ���һ��B�ͳ���20��Ԫ������2��A�ͳ��ȹ���3��B�ͳ���60��Ԫ��
�����������飬����һ��A�ͳ��ȹ���һ��B�ͳ���20��Ԫ������2��A�ͳ��ȹ���3��B�ͳ���60��Ԫ��
![]() �����a��b��
�����a��b��
![]() ������������϶���������ÿ���ܽ�ʡ
������������϶���������ÿ���ܽ�ʡ![]() �������ͣ�����������϶�����������Ҫ������Ԫ��
�������ͣ�����������϶�����������Ҫ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����DCB�У���A=��D=90�㣬AC=BD��AC��BD�ཻ�ڵ�O.
(1)��֤����ABC�ա�DCB��
(2)��OBC�Ǻ��������Σ�֤����Ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����ֱ�Ƕ���
����ֱ�Ƕ���![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶������
��Ϊ�뾶������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() ���ܳ��ú�
���ܳ��ú�![]() �Ĵ���ʽ��ʾΪ_______________��
�Ĵ���ʽ��ʾΪ_______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ǹ��Ϊ8��8�������������������������а�����Ҫ�������
(1)�������н���ƽ��ֱ������ϵ��ʹA������Ϊ(-2��4)��B������Ϊ(-4��2)��
(2)��(1)��ǰ���£��ڵڶ������ڵĸ������һ��C��ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ�������������������C��������ǣ�
(3)��((2)�С�ABC���ܳ�(�����������)��
(4)����((2)����ABC����y��ԳƵ���A'B'C'.
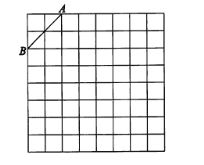
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У��߳�Ϊ
�У��߳�Ϊ![]() ��������
��������![]() �Ķ���
�Ķ���![]() ��
��![]() �ֱ���
�ֱ���![]() �������ᡢ
�������ᡢ![]() ��ĸ������ϣ����κ���
��ĸ������ϣ����κ���![]() ��ͼ��
��ͼ��![]() ��
��![]() ���㣮
���㣮

![]() ��ö��κ����Ķ������ꣻ
��ö��κ����Ķ������ꣻ
![]() ��Ϻ�����ͼ��̽������
��Ϻ�����ͼ��̽������![]() ʱ
ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
![]() ��
��![]() ����
����![]() ��
��![]() ���㶼�ڸú���ͼ���ϣ��ԱȽ�
���㶼�ڸú���ͼ���ϣ��ԱȽ�![]() ��
��![]() �Ĵ�С������Ҫ˵�����ɣ�
�Ĵ�С������Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı��� ABCD �У���C=70������B=��D=90����E��F �ֱ��� BC��DC �ϵĵ㣬����AEF ���ܳ���Сʱ����EAF �Ķ���Ϊ����

A.30��B.40��C.50��D.70��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com