
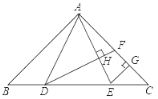
【题目】如图,在△ABC中,AB=AC,点D、E在线段BC上,且BE=CD,连接AD、AE,过点D作DF⊥AE,垂足为H,交AC于点F,过点E作EG⊥AC,垂足为G.
(1)若DH=4,AD=5,HF=1,求AF的长;
(2)若∠BAC=90°,求证:AF=2CG.
【答案】(1)AF=![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)在Rt△ADH中,根据勾股定理可以求得AH的长,继而在Rt△AHF中,利用勾股定理求得AF长即可;
(2)作DM⊥AC于M,证明△ABE≌△ACD,△DAM≌△AEG,继而可得△GEC是等腰直角三角形,再等腰三角形的性质即可得.
(1)在Rt△ADH中,∵AD=5,DH=4,
∴AH=![]() =3,
=3,
在Rt△AHF中,AF=![]() ;
;
(2)作DM⊥AC于M,
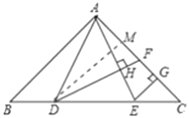
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°
∵BE=CD,
∴△ABE≌△ACD,
∴AD=AE,∠BAE=∠CAD,
∴∠CAE=∠BAD,
∵AE⊥DF,
∴∠AHF=90°,
∵∠DAF=90°﹣∠BAD,∠DFA=90°﹣∠CAE,
∴∠DAF=∠DFA,
∴DA=DF,
∴AE=AD,
∵AB∥DM,∴∠ADM=∠BAD=∠EAG,
∵∠AMD=∠AGE=90°,
∴△DAM≌△AEG,
∴AM=GE,
∵∠C=45°,EG⊥AC,
∴△GEC是等腰直角三角形,
∴EG=CD,
∵AD=DF,DM⊥AF,
∴AM=FM,
∴AF=2CG.


科目:初中数学 来源: 题型:
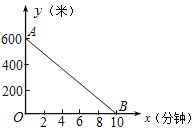
【题目】小明、小军是同班同学.某日,两人放学后去体育中心游泳,小明16:00从学校出发,小军16:03也从学校出发,沿相同的路线追赶小明.设小明出发x分钟后,与体育中心的距离为y米.如图,线段AB表示y与x之间的函数关系.
(1)求y与x之间的函数解析式;(不要求写出定义域)
(2)如果小军的速度是小明的1.5倍,那么小军用了多少分钟追上小明?此时他们距离体育中心多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒.已知A、B两种礼盒的单价比为2:3,单价和为200元;
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主进这两种礼盒花费不超过9720元,B种礼盒的数量是A种礼盒数量的2倍多1个,且B种礼盒的数量不低57个,共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
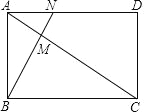
【题目】如图,已知矩形 ABCD 中,AB=1,BC=![]() ,点 M 在 AC 上,且 AM=
,点 M 在 AC 上,且 AM=![]() AC,连接并延长 BM 交 AD 于点 N.
AC,连接并延长 BM 交 AD 于点 N.
(1)求证:△ABC∽△AMB;
(2)求 MN 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
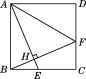
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
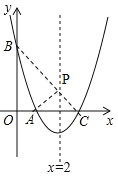
【题目】如图,抛物线![]() 交x轴于点
交x轴于点![]() ,交y轴于点B,对称轴是直线
,交y轴于点B,对称轴是直线![]() .
.
(1)求抛物线的解析式;
(2)P是抛物线对称轴上的一个动点,是否存在点P,使![]() 的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com