分析:根据平行四边形的性质判断即可;根据矩形的性质和三角形的内角和定理求出∠E=∠EFG=∠G=90°,得出矩形,证△AFB和△DHC全等,求出EF=EH,即可判断B;根据菱形的性质判断即可;根据平行四边形的判定和等腰梯形的判定判断即可.
解答:解:A、平行四边形的对角线互相平分,故本选项错误;
B、如图:
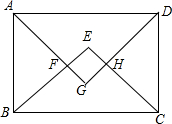
∠EBC+∠ECB=45°+45°=90°,
∴∠E=180°-90°=90°,
同理∠G=∠AFB=∠DHC=90°,
∴∠E=∠EFG=∠G=90°,
∴四边形EFGH是矩形,
∵∠EBC=∠ECB=45°,
∴BE=CE,
在△AFB和△DHC中
,
∴△AFB≌△DHC,
∴BF=CH,
∵BE=CE,
∴EF=EH,
∴矩形EFGH是正方形,故本选项错误;
C、菱形的对角线互相垂直平分,故本选项错误;
D、一组对边相等,另一组对边平行的四边形可能是等腰梯形,也可能是平行四边形,故本选项正确.
故选D.
点评:本题考查了对平行四边形的性质和判定,梯形的性质,菱形的性质,三角形的内角和定理,全等三角形的性质和判定,等腰三角形的性质等知识点的综合运用,题目综合性比较强,也较好,难度适中,主要检查学生能否运用性质进行说理和判断.




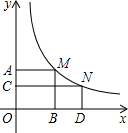 如图,点M,N在反比例函数y=
如图,点M,N在反比例函数y=