画出函数y=2x-1的图象．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

17．画出函数y=2x-1的图象．

分析根据一次函数的图象是直线，只需确定直线上两个特殊点即可．

解答解：直线y=2x-1经过点（0，-1），（$\frac{1}{2}$，0），图象如图所示：

点评本题考查一次函数、正比例函数的图象的作法，解题的关键是一次函数的图象是直线，确定两点即可画出直线，属于中考常考题型．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

7．

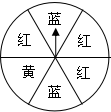如图，一个可以自由转动的转盘被等分成6个扇形区域，并涂上了相应的颜色，转动转盘，转盘停止后，指针指向红色区域的概率是（　　）

A．

$\frac{2}{3}$

B．

$\frac{1}{2}$

C．

$\frac{1}{3}$

D．

$\frac{1}{6}$

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．

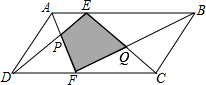如图，在?ABCD中，E、F分别是AB、DC边上的点，AF与DE相交于点P，BF与CE相交于点Q，若S_△APD=16cm²，S_△BQC=25cm²，则图中阴影部分的面积为41cm²．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．

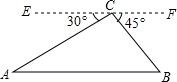如图，从热气球C处测得地面A，B两点的俯角分别为30°，45°，此时热气球C处所在位置到地面上点A的距离为400米．求地面上A，B两点间的距离．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．

右图是由六个完全相同的小正方体组合而成的立体图形，它的主视图是（　　）

A．

B．

C．

D．

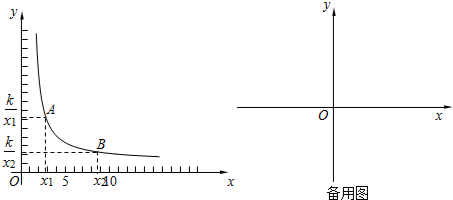
查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．【课本节选】
反比例函数y=$\frac{k}{x}$（k为常数，k≠0）的图象是双曲线．当k＞0时，双曲线两个分支分别在一、三象限，在每一个象限内，y随x的增大而减小（简称增减性）；反比例函数的图象关于原点对称（简称对称性）．
这些我们熟悉的性质，可以通过说理得到吗？
【尝试说理】
我们首先对反比例函数y=$\frac{k}{x}$（k＞0）的增减性来进行说理．
如图，当x＞0时．
在函数图象上任意取两点A、B，设A（x₁，$\frac{k}{{x}_{1}}$），B（x₂，$\frac{k}{{x}_{2}}$），
且0＜x₁＜x₂．
下面只需要比较$\frac{k}{{x}_{1}}$和$\frac{k}{{x}_{2}}$的大小．
$\frac{k}{{x}_{2}}$-$\frac{k}{{x}_{1}}$=$\frac{k（{x}_{1}-{x}_{2}）}{{{x}_{1}x}_{2}}$
∵0＜x₁＜x₂，∴x₁-x₂＜0，x₁x₂＞0，且 k＞0．
∴$\frac{k（{x}_{1}-{x}_{2}）}{{{x}_{1}x}_{2}}$＜0．即$\frac{k}{x_2}$＜$\frac{k}{x_1}$．
这说明：x₁＜x₂时，$\frac{k}{{x}_{1}}$＞$\frac{k}{{x}_{2}}$．也就是：自变量值增大了，对应的函数值反而变小了．
即：当x＞0时，y随x的增大而减小．同理，当x＜0时，y随x的增大而减小．
（1）试说明：反比例函数y=$\frac{k}{x}$ （k＞0）的图象关于原点对称．
【运用推广】
（2）分别写出二次函数y=ax² （a＞0，a为常数）的对称性和增减性，并进行说理．
对称性：二次函数y=ax²（a＞0，a为常数）的图象关于y轴成轴对称；
增减性：当x＞0时，y随x增大而增大；当x＜0时，y随x增大而减小．．
说理：①∵在二次函数y=ax²（a＞0，a为常数）的图象上任取一点Q（m，n），于是n=am²．
∴点Q关于y轴的对称点Q₁（-m，n）．
而n=a（-m）²，即n=am²．
这说明点Q₁也必在在二次函数y=ax²（a＞0，a为常数）的图象上．
∴二次函数y=ax²（a＞0，a为常数）的图象关于y轴成轴对称；
②在二次函数y=ax²（a＞0，a为常数）的图象上任取两点A、B，
设A（m，am²），B（n，an²），且0＜m＜n．
则an²-am²=a（n+m）（n-m），
∵n＞m＞0，
∴n+m＞0，n-m＞0；
∵a＞0，
∴an²-am²=a（n+m）（n-m）＞0，即an²＞am²．
而当m＜n＜0时，n+m＜0，n-m＞0；
∵a＞0，
∴an²-am²=a（n+m）（n-m）＜0．即an²＜am²．
这说明，当x＞0时，y随x增大而增大；当x＜0时，y随x增大而减小；．
【学以致用】
（3）对于函数y=x²+$\frac{2}{x}$ （x＞0），
请你从增减性的角度，请解释为何当x=1时函数取得最小值．