
【题目】某校积极开展“阳光体育进校园”活动,决定开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目,规定每个学生必须参加一项活动。学校为了了解学生最喜欢哪一种运动项目,设计了以下四种调查方案.
方案一:调查该校七年级女生喜欢的运动项目
方案二:调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目
方案三:调查该校书法小组的学生喜欢的运动项目
方案四:调查该校田径队的学生喜欢的运动项目
(1)上面的调查方案最合适的是 ;
学校体育组采用了(1)中的方案,将调查的结果绘制成如下两幅不完整的统计图表.
最喜欢的运动项目人数调查统计表 最喜欢的运动项目人数分布统计图


请你结合图表中的信息解答下列问题:
(2)这次抽样调查的总人数是 ,m= ;
(3)在扇形统计图中,A 项目对应的圆心角的度数为 ;
(4)已知该校有 1200 名学生,请根据调查结果估计全校学生最喜欢乒乓球的人数.
【答案】(1)方式二;(2)80人,8;(3)162°;(4)540人
【解析】
(1)根据抽样调查的数据需要具有代表性解答可得;
(2)根据样本中最喜欢B(篮球)项目的人数20人,所占百分比25%得出抽样调查的总人数,用总人数减去其他项目的人数即可求得m
(3)利用样本中最喜欢A(乒乓球)项目的人数36人除以总人数,得出最喜欢A(乒乓球)项目所占的百分比,求出后再乘以360度即可求出度数;
(4)用全校学生数×选乒乓球的学生所占百分比即可.
解:(1)上面的调查方式合适的是方式二,
故答案为:方式二;
(2)20÷25%=80(人)
∴这次抽样调查的总人数是80人
m=80-36-20-16=8
故答案为:80人,8
(3)360°×![]() =162°,
=162°,
∴A 项目对应的圆心角的度数为162°
故答案为:162°.
(4)1200×![]() =540(人),
=540(人),
答:估计全校学生最喜欢乒乓球的人数为540人.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在![]() 轴上,记为
轴上,记为![]() ,折痕为CE.直线CE的关系式是
,折痕为CE.直线CE的关系式是![]() ,与
,与![]() 轴相交于点F,且AE=3.
轴相交于点F,且AE=3.
(1)求OC长度;
(2)求点![]() 的坐标;
的坐标;
(3)求矩形ABCO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
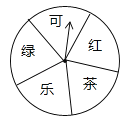
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
学校给七年级学生组织知识竞赛,共设20道题,各题的分值相同,每题必答.下表记录了5名学生的得分情况
参赛者 | 答对题数 | 答错题数 | 得分 |
小明 | 10 | 10 | 40 |
小红 | 19 | 1 | 94 |
小刚 | 20 | 0 | 100 |
小强 | 18 | 2 | 88 |
小丽 | 14 | 6 | 64 |
(1)参赛者小芳得76分,她答对了几道题?
(2)参赛者小花说她得了83分,你认为可能吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学参加1 000米比赛,由于参赛选手较多,将选手随机分A、B、C三组进行比赛.
(1)甲同学恰好在A组的概率是________;
(2)求甲、乙两人至少有一人在B组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC中,∠BAC=120°,AB=AC=6,点D为边BC上一动点.将△ABD沿着AD对折到△AB′D.若△BB′D为直角三角形,则BD=___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,先按要求画图形,再解决问题.
的中点,先按要求画图形,再解决问题.
(1)延长线段![]() 至点
至点![]() ,使
,使![]() ;延长线段
;延长线段![]() 至点
至点![]() ,使
,使![]() ;(尺规作图,保留作图痕迹)
;(尺规作图,保留作图痕迹)
(2)求线段![]() 的长度;
的长度;
(3)若点![]() 是线段
是线段![]() 的中点,求线段
的中点,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com