
【题目】如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
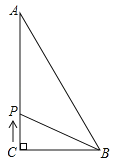
(1)当t= 时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是![]() = .
= .
(3)若△BPC的面积为18,试求t的值.
【答案】(1)6.5秒;(2)1:4;(3)t=![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)根据中线的性质可知,点P在AB中点时,CP把△ABC的面积分成相等的两部分,列出方程求解即可;
(2)求出当t=5时,AP与BP的长,再根据等高的三角形面积比等于底边的比求解即可;
(3)分两种情况:①P在AC上;②P在AB上,分别根据三角形面积公式建立关于t的方程,求解可得.
解:(1)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,
此时CA+AP=12+7.5=19.5,
∴3t=19.5,
解得t=6.5,
故当t=6.5秒时,CP把△ABC的面积分成相等的两部分;
(2)∵5×3=15,
∴AP=1512=3,BP=153=12,
则S△APC:S△BPC=3:12=1:4;
(3)分两种情况:
①当P在AC上时,
∵△BPC的面积为18,
∴![]() ×9×CP=18,
×9×CP=18,
∴CP=4,
∴3t=4,t=![]() ;
;
②当P在AB上时,
∵△BPC的面积为18,△ABC的面积为![]() ,
,
∴△BPC的面积是△ABC面积的![]() ,
,
∴3t=12+15×![]() ,
,
解得:t=![]() ,
,
故t=![]() 秒或
秒或![]() 秒时,△BPC的面积为18.
秒时,△BPC的面积为18.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究.对数轴上的任意一点P.
①作出点N使得N和P表示的数互为相反数,再把N对应的点向右平移1个单位,得到点P的对应点P′.我们称P′是P的N变换点;
②把P点向右平移1个单位,得到点M,作出点P′′使得P′′和M表示的数互为相反数,我们称P′′是P的M变换点.
(1)如图,若点P表示的数是-4,则P的N变换点P′表示的数是 ________ ;

(2)若P的M变换点P′′表示的数是2,则点P表示的数是 ________ ;
(3)若P′,P′′分别为P的N变换点和M变换点,且OP′=2OP′′,求点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
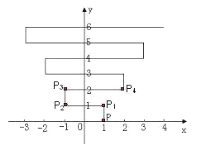
【题目】如下图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位…,依此规律跳动下去,点P第2019次跳动至点P2019的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com