
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() 的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )

①AD是∠BAC的平分线; ②∠ADC=60°;
③点D在线段ABC的垂直平分线上; ④BD=2CD.
A. 2个 B. 3个 C. 1个 D. 4个
【答案】D
【解析】
根据“角平分线的尺规作法”结合“已知条件”进行分析判断即可.
(1)由题意可知,图中的尺规作图,作的是∠BAC的角平分线,故结论①成立;
(2)∵在△ABC中,∠C=90°,∠B=30°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠CAD=∠BAD=30°,
∴∠ADC=180°-90°-30°=60°,故结论②成立;
(3)∵∠BAD=30°,∠B=30°,
∴∠BAD=∠B,
∴AD=BD,
∴点D在AB的垂直平分线上,故结论③成立;
(4)∵在△ACD中,∠ACD=90°,∠CAD=30°,
∴AD=2CD,
∵AD=BD,
∴BD=2CD,故结论④成立;
综上所述,题中4个结论都成立.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB//CD,AD//BC,E,F是对角线BD上的两点,如果添加一个条件使![]() ,则添加的条件不能是( )
,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台“幸运 52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
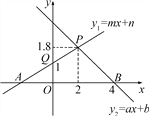
【题目】如图,根据图中信息解答下列问题:
(1)关于x的不等式ax+b>0的解集是________;
(2)关于x的不等式mx+n<1的解集是________;
(3)当x为何值时,y1≤y2?
(4)当x<0时,比较y2与y1的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:

(1)斜边AB的长;
(2)△ABC的面积;
(3)高CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
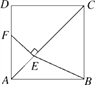
【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com