
����Ŀ����1����ͼ��1������֪���ڵ���ֱ��������![]() �У�
�У�![]() ��ֱ��
��ֱ��![]() ������
������![]() ��
��![]() ֱ��
ֱ��![]() ��
��![]() ֱ��
ֱ��![]() ������ֱ�Ϊ��
������ֱ�Ϊ��![]() ��
��![]() .��
.��![]() ��
��![]() ��
��![]() ֮���������ϵ�ǣ� .
֮���������ϵ�ǣ� .
��2����ͼ��2��������1���е�������Ϊ���ڵ���������![]() �У�
��![]() ��
��![]() ��
��![]() ���㶼��ֱ��
���㶼��ֱ��![]() �ϣ���
�ϣ���![]() ������
������![]() Ϊ������ǻ�۽�.���ʽ���
Ϊ������ǻ�۽�.���ʽ���![]() �Ƿ��������������������֤����������������˵������.
�Ƿ��������������������֤����������������˵������.
��3����չ��Ӧ�ã���ͼ��3����![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϵ������㣨
�ϵ������㣨![]() ��
��![]() ��
��![]() ���㻥���غϣ�����
���㻥���غϣ�����![]() Ϊ
Ϊ![]() ƽ�����ϵ�һ�㣬��
ƽ�����ϵ�һ�㣬��![]() ��
��![]() ��Ϊ�ȱ������Σ�����
��Ϊ�ȱ������Σ�����![]() ��
��![]() ����
����![]() ����֤��
����֤��![]() .
.

���𰸡���1��DE=BD+CE����2����������3�����ɼ�������
��������
��1������ͬ�ǵ������ȵó���CAE=��ABD����������AAS�ó���ABD�ա�CAE�����ɵó�DE=BD+CE��
��2�����ݡ�BDA=��AEC=��BAC=�����ó���CAE=��ABD���ڡ�ADB�͡�CEA�У�����AAS֤����ADB�ա�CEA���Ӷ��ó�AE=BD��AD=CE������֤��DE=BD+CE��
��3������BC���ɣ�2���Ľ��۵õ���ADB�ա�CEA����BD=AE����DBA=��CAE�����ݵȱ������ε����ʵá�ABF=��CAF=60�㣬���С�DBF=��FAE�����á�SAS����֤����DBF�ա�EAF�����ɵó����ۣ�
��1��DE=BD+CE���������£�
��ͼ1��
��BD��l��CE��l�����BDA=��AEC=90�㣮
�֡ߡ�BAC=90�㣬���BAD+��CAE=90�㣬��BAD+��ABD=90�㣬���CAE=��ABD��
�ڡ�ABD�͡�CAE�У��� �����ABD�ա�CAE��AAS������BD=AE��AD=CE��
�����ABD�ա�CAE��AAS������BD=AE��AD=CE��
��DE=AD+AE����DE=CE+BD��
��2���������������£�
��ͼ2��
�ߡ�BDA=��AEC=��BAC=�������DBA+��BAD=��BAD+��CAE=180�㩁�������CAE=��ABD��
�ڡ�ADB�͡�CEA�У���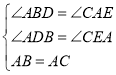 �����ADB�ա�CEA��AAS������AE=BD��AD=CE����BD+CE=AE+AD=DE��
�����ADB�ա�CEA��AAS������AE=BD��AD=CE����BD+CE=AE+AD=DE��
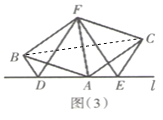
��3��DF=EF���������£�
����BC��
�ߡ�ABF�͡�ACF��Ϊ�ȱ������Σ���BF=BA=AF=AC����ABF=��CAF=60�㣮
�ɣ�2��֪����ADB�ա�CAE��BD=EA����DBA=��CAE��
�ߡ�ABF=��CAF=60�㣬���DBA+��ABF=��CAE+��CAF�����DBF=��FAE��
�ڡ�DBF�͡�EAF�У���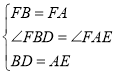 �����DBF�ա�EAF��SAS������DF=EF��
�����DBF�ա�EAF��SAS������DF=EF��


 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з������Ӧ���⣺���조һ��һ·�����ʺ����߷���̳�ٰ�֮��ij��˾�������ס���������Ʒ������һ��һ·�����߹��Һ͵�����ԭ�ƻ���������Ʒ������Ʒ��210�֣������¼�����ʵ�ʲ���Ϊ230�֣����м���Ʒ����5%������Ʒ����15%����ù�˾ʵ�������ס���������Ʒ�����ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
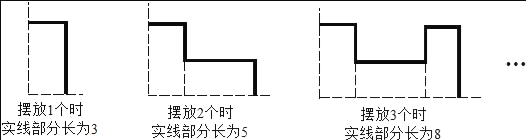
����Ŀ������ͬ�ľ��ο�Ƭ������ͼ��ʽ�ڷ���һ��ֱ���ϣ�ÿ�����ο�Ƭ��Ϊ2����Ϊ1���������ƣ��ڷ�2014��ʱ��ʵ�߲��ֳ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��õ�����������ˮ�ʣ����������������۹�˾�������� 10 ̨��ˮ�����豸������ A��B �����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±���
A �� | B �� | |
�۸���Ԫ/̨�� | a | b |
������ˮ�����֣��£� | 240 | 200 |
�����飺����һ̨ A ���豸�ȹ���һ̨ B ���豸�� 2 ��Ԫ������ 2 ̨ A ���豸�ȹ��� 3 ̨ B ���豸�� 6 ��Ԫ��
��1���� a��b ��ֵ��
��2����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ��� 105 ��Ԫ������Ϊ�ù�˾ ���ļ��ֹ�����
��3���ڣ�2���ʵ������£���ÿ��Ҫ��������������ˮ�������� 2040 �֣�Ϊ�˽� Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��������![]() �У�
�У�![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��
��1����![]() ʱ����ͼ�٣��ֱ����
ʱ����ͼ�٣��ֱ����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����֤��
����֤��![]() ��
��
��2����![]() ��
��![]() ʱ����ͼ�ڣ���
ʱ����ͼ�ڣ���![]() ���
���![]() ����ֱ��
����ֱ��![]() �Գƣ�����
�Գƣ�����![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������ÿ��1����λ���ȵ��ٶ���
��������ÿ��1����λ���ȵ��ٶ���![]() �����յ�
�����յ�![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������ÿ��3����λ���ٶ���
��������ÿ��3����λ���ٶ���![]() ���յ�
���յ�![]() �˶�����
�˶�����![]() ��
��![]() ������Ӧ���յ�ʱֹͣ�˶�������
������Ӧ���յ�ʱֹͣ�˶�������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() �����˶�ʱ��Ϊ
�����˶�ʱ��Ϊ![]() �룮
�룮
���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��
��ֱ��д����![]() ��
��![]() ȫ��ʱ
ȫ��ʱ![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ���x2-2��m��1��x��m2=0.
��1����mȡ��ֵʱ������������ʵ������
��2��Ϊmѡȡһ�����ʵ�������ʹ��������������ȵ�ʵ��������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���mx2��2mx��m��2��0.
(1)����������������ʵ��������m��ȡֵ��Χ��
(2)�����̵���ʵ����Ϊx1��x2����|x1��x2|��1����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ��������Ӧ����.
2000�����������ǶԹ��ɶ�����֤���ĸ���Ȥ��������Ϊ���������Ҫ������������Ϊ��������������ǵ�����ʵ�ʣ����Ժܶ��˶�̽�֡��о�����֤�����µ�֤�����ϳ���.
�����ͼ���Ǵ�˵�бϴ����˹��֤��ͼ�Σ�
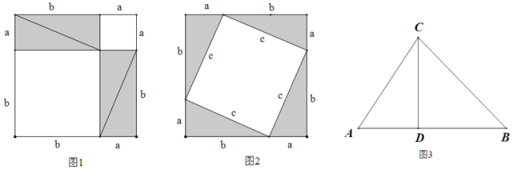
֤��������ͼ1�У���![]()
![]() 4��ֱ�������ε����+���������ε����
4��ֱ�������ε����+���������ε����
=4�� + + .
����ͼ2�У���![]()
![]() 4��ֱ�������ε����+�����ε����
4��ֱ�������ε����+�����ε����
=4�� + .
��4�� + + =4�� + .
�����ã�![]()
�� .
����1���������еĿ�ȱ���ֲ���������
��2����ͼ3������ABC�У���A=60��,��ACB=75����CD��AB��AC=4����BC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ı���![]() �У�
�У�![]() Ϊ�ı���
Ϊ�ı���![]() ��
��![]() ��ƽ�������
��ƽ�������![]() ��ƽ�������ڵ�ֱ�߹��ɵ���ǣ���
��ƽ�������ڵ�ֱ�߹��ɵ���ǣ���![]() ��
��![]() ��
��
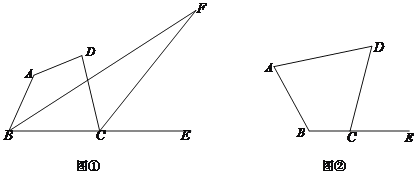
(1)��ͼ�٣���![]() ��180��ʱ��
��180��ʱ��![]() =_________(�ú�
=_________(�ú�![]() ��
��![]() ��ʽ�ӱ�ʾ)��
��ʽ�ӱ�ʾ)��
(2)��ͼ�ڣ���![]() ��180��ʱ������ͼ���У�����
��180��ʱ������ͼ���У�����![]() ����
����![]() ______(�ú�
______(�ú�![]() ��
��![]() ��ʽ�ӱ�ʾ)��
��ʽ�ӱ�ʾ)��
(3)��![]() ��
��![]() ��������_______ʱ��������
��������_______ʱ��������![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com