
 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
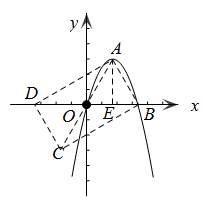
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
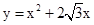 ;(3)
;(3)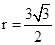 或
或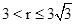 .
.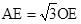 .∴
.∴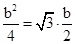 (b﹥0).∴
(b﹥0).∴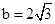 .
.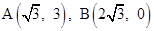 .
. .
.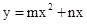 ,则
,则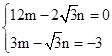 ,解之,得
,解之,得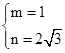 .
.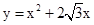 .
.
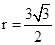 .
.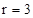 .
.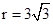 .
.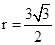 或
或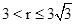 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
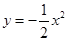 分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .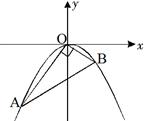
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
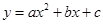 交
交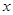 轴于A、B两点(点A在点B左侧),与
轴于A、B两点(点A在点B左侧),与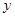 轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线
轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线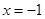 交
交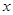 轴于点E,点D为顶点.
轴于点E,点D为顶点.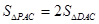 ,,求点P的坐标;
,,求点P的坐标;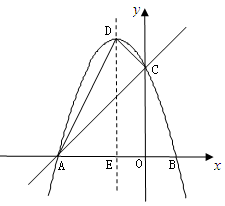
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线 上.
上. 的解析式;
的解析式; ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
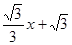 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点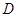 是劣弧AO上一动点(
是劣弧AO上一动点(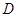 点与
点与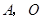 不重合).抛物线y=-
不重合).抛物线y=-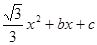 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,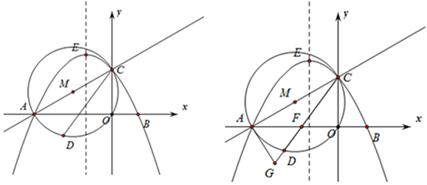
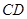 交
交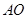 于点
于点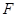 ,延长
,延长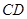 至
至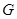 ,使
,使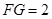 ,试探究当点
,试探究当点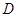 运动到何处时,直线
运动到何处时,直线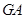 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
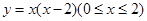 的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .
的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .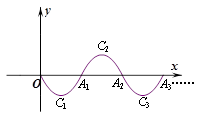
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),则下列结论正确的是( )
的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),则下列结论正确的是( )
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com