
【题目】若函数![]() 是
是![]() 关于
关于![]() 的反比例函数。
的反比例函数。
(1)求![]() 的值;
的值;
(2)函数图象在哪些象限?在每个象限内,![]() 随
随![]() 的增大而怎样变化?
的增大而怎样变化?
(3)当![]() 时,求
时,求![]() 的取值范围。
的取值范围。
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为了贯彻落实国家关于增强青少年体质的计划,我市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程.某牛奶供应商拟提供A(原味)、B(草莓味)、C(核桃味)、D(菠萝味)、E(香橙味)等五种口味的学生奶供学生选择(所有学生奶盒形状、大小相同),为了解对学生奶口味的喜好情况,某初级中学九年级(1)班张老师对全班同学进行了调查统计,制成了如图所示的两幅不完整的统计图.
(1)该班共有多少人?
(2)求出喜好A和E学生奶口味的人数;
(3)该班五种口味的学生奶喜好人数组成一组统计数据,求出这组数据的平均数;
(4)将折线统计图补充完整.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系;![]() 表示摩托车厂一天的销售成本与销售量的关系.
表示摩托车厂一天的销售成本与销售量的关系.

(1)写出销售收入与销售量之间的函数关系式;
(2)写出销售成本与销售量之间的函数关系式;
(3)当一天的销售量为多少辆时,销售收入等于销售成本;
(4)当一天的销售超过多少辆时,工厂才能获利? (利润=收入成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级、B级、C级、D级),并将那个测试结果绘成了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:

(1)本次抽样测试的学生人数是 ;
(2)扇形图中∠α的度数是 ,并把条形统计图补充完整;
(3)对A,B,C,D四个等级依次赋分为90,75,65,55(单位:分),比如:等级为A的同学体育得分为90分,…,依此类推.该市九年级共有学生32000名,如果全部参加这次体育测试,估计该市九年级不及格(即60分以下)学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.
(1)当2≤x≤6时,求y与x的表达式;
(2)请将图象补充完整;
(3)从进水管开始进水起,求该容器内的水量不少于7.5升所持续时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
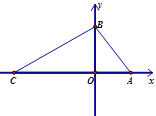
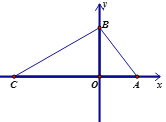
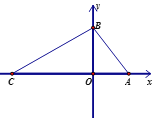
【题目】如图,在平面直角坐标系中,O为坐标原点,A(a,0),B(0,b),且a,b满足![]() ,连接AB,AB=5.C(-7,0)是x轴负半轴上一点,连接BC.
,连接AB,AB=5.C(-7,0)是x轴负半轴上一点,连接BC.
(1)求OA、OB的长;
(2)动点P从点B出发,沿BA以每秒2个单位的速度向终点A匀速运动,连接CP,设点P的运动时间为t,△CBP的面积为S,用含t的代数式表示S(不要求写出t的取值范围)
(3)在(2)的条件下,连接OP,是否存在t值,使S△BCP=![]() S△PCO,如果存在,求出相应的t值,并直接写出P点坐标.若不存在,说明理由.
S△PCO,如果存在,求出相应的t值,并直接写出P点坐标.若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com