
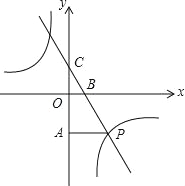
【题目】如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
【答案】(1)反比例函数的表达式为y=﹣![]() ;
;
(2)点Q的坐标为(﹣![]() ,9)或(
,9)或(![]() ,﹣3).
,﹣3).
【解析】
试题分析:(1)由一次函数表达式可得出点C的坐标,结合A点坐标以及三角形的面积公式可得出AP的长度,从而得出点P的坐标,由点P的坐标结合待定系数法即可求出一次函数及反比例函数的表达式;
(2)设点Q的坐标为(m,﹣![]() m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
试题解析:(1)令一次函数y=kx+3中的x=0,则y=3,
即点C的坐标为(0,3),
∴AC=3﹣(﹣6)=9.
∵S△CAP=![]() ACAP=18,
ACAP=18,
∴AP=4,
∵点A的坐标为(0,﹣6),
∴点P的坐标为(4,﹣6).
∵点P在一次函数y=kx+3的图象上,
∴﹣6=4k+3,解得:k=﹣![]() ;
;
∵点P在反比例函数y=![]() 的图象上,
的图象上,
∴﹣6=![]() ,解得:n=﹣24.
,解得:n=﹣24.
∴一次函数的表达式为y=﹣![]() x+3,反比例函数的表达式为y=﹣
x+3,反比例函数的表达式为y=﹣![]() .
.
(2)令一次函数y=﹣![]() x+3中的y=0,则0=﹣
x+3中的y=0,则0=﹣![]() x+3,解得:x=
x+3,解得:x=![]() ,
,
即点B的坐标为(![]() ,0).设点Q的坐标为(m,﹣
,0).设点Q的坐标为(m,﹣![]() m+3).
m+3).
∵△OCQ的面积是△BCO面积的2倍,
∴|m|=2×![]() ,解得:m=±
,解得:m=±![]() ,
,
∴点Q的坐标为(﹣![]() ,9)或(
,9)或(![]() ,﹣3).
,﹣3).


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】“老牛:累死我了!
小马:你还累?这么大的个,才比我多驮了2个.
老牛:哼,我从你背上拿来1个,我的包裹数就是你的2倍!
小马:真的?!”
根据老牛和小马的对话,你能求出它们各驮了多少个包裹吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天安门广场的面积约为44万平方米,请你估计一下,它的百万分之一大约相当于( )
A. 教室地面的面积 B. 黑板面的面积 C. 课桌面的面积 D. 铅笔盒盒面的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com