
【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④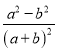 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()

小强: ![]()
![]()
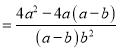
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上![]() 含6个
含6个![]() 为合格,做9个以上
为合格,做9个以上![]() 含9个
含9个![]() 为优秀,两组同学的测试成绩如下表:
为优秀,两组同学的测试成绩如下表:
成绩 | 4 | 5 | 6 | 7 | 8 | 9 |
甲组 | 1 | 2 | 5 | 2 | 1 | 4 |
乙组 | 1 | 1 | 4 | 5 | 2 | 2 |
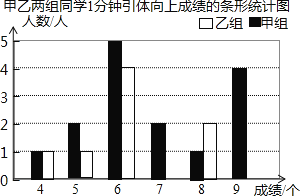
现将两组同学的测试成绩绘制成如下不完整的统计图表:
统计量 | 平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲组 | a | 6 | 6 |
|
|
|
乙组 |
| b | 7 |
|
|
|
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 统计表中的
统计表中的![]() ______,
______,![]() ______;
______;
![]() 人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
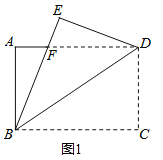
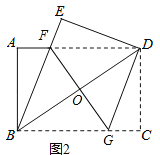
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:BF=DF;
(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.
①求证:四边形BFDG是菱形;
②若AB=3,AD=4,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,∠A=60°,BD⊥AC于点D,DG∥AB,DG交BC于点G,点E在BC的延长线上,且CE=CD.
(1)求∠ABD和∠BDE的度数;
(2)写出图中的等腰三角形(写出3个即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com