
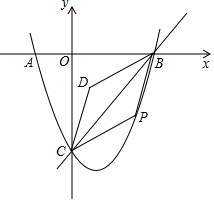
 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作?CPBD,设?CPBD的面积为S,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作?CPBD,设?CPBD的面积为S,点P的横坐标为m.分析 (1)利用交点式求抛物线的解析式;
(2)先确定点D在x轴上,再利用平行四边形的性质可判断PC∥x轴,然后根据抛物线的对称性确定点P的坐标;
(3)作PQ∥y轴交直线BC于Q,如图1,利用待定系数法求出直线BC的解析式为y=x-3,设P(m,m2-2m-3),则Q(m,m-3),讨论:当0<m<3时,如图1,PQ=-m2+3m,利用三角形面积公式和平行四边形的性质得S=2S△PBC=2(S△PQC+S△PQB)=-3m2+9m;当m<0或m>3时,如图2,PQ=m2-3m,同理可得S=2S△PBC=2(S△PBQ-S△PQC)=3m2-9m;
(4)讨论:当点P在x轴下方,如图3,CD交x轴于E,利用已知条件得到S△DEB:S平行四边形CPBD=1:8,再根据平行四边形的性质得S△DEB:S△BCE=1:3,接着根据三角形面积公式得到D点的纵坐标为1,然后利用点平移的坐标规律得到点C向下平移1个单位可得到P点,即P点的纵坐标为-4,则解方程x2-2x-3=-4可得到对应m的值;当点P在x轴上方,如图4,CP交x轴于E,同理可得点P到x轴的距离为1,即P点的纵坐标为1,则通过解方程x2-2x-3=1可得对应m的值.
解答 解:(1)抛物线的解析式为y=(x+1)(x-3),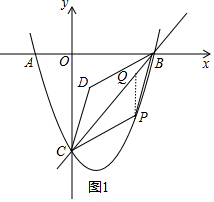
即y=x2-2x-3;
(2)∵?CPBD有两个顶点在x轴上,
∴点D在x轴上,
而BD∥PC,
∴点P和点C为抛物线上的对称点,
而抛物线的对称轴为直线x=1,
∴点P的坐标为(2,-3);
(3)作PQ∥y轴交直线BC于Q,如图1,
设直线BC的解析式为y=kx+b,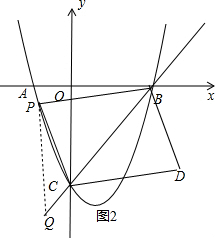
把C(0,-3),B(3,0)代入得$\left\{\begin{array}{l}{b=-3}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴直线BC的解析式为y=x-3,
设P(m,m2-2m-3),则Q(m,m-3),
当0<m<3时,如图1,PQ=m-3-(m2-2m-3)=-m2+3m
S=2S△PBC=2(S△PQC+S△PQB)=2•$\frac{1}{2}$•3•(-m2+3m)=-3m2+9m;
当m<0或m>3时,如图2,PQ=m2-2m-3-(m-3)=m2-3m
S=2S△PBC=2(S△PBQ-S△PQC)=2•$\frac{1}{2}$•3•(m2-3m)=3m2-9m;
(4)当点P在x轴下方,如图3,CD交x轴于E,
∵x轴将?CPBD的面积分成1:7两部分,
∴S△DEB:S平行四边形CPBD=1:8,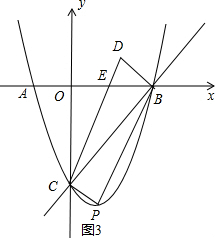
∴S△DEB:S△BCD=1:4,
∴S△DEB:S△BCE=1:3,
而OC=3,
∴点D到x轴的距离为1,即D点的纵坐标为1,
∵四边形CPBD为平行四边形,
∴点C向下平移1个单位可得到P点,即P点的纵坐标为-4,
当x=-4时,x2-2x-3=-4,解得x1=x2=1,则P点坐标为(1,-4),
∴m=1;
当点P在x轴上方,如图4,CP交x轴于E,
∵x轴将?CPBD的面积分成1:7两部分,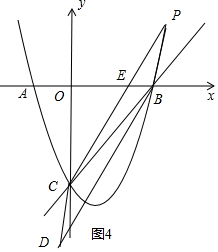
∴S△PEB:S平行四边形CPBD=1:8,
∴S△PEB:S△BCP=1:4,
∴S△PEB:S△BCE=1:3,
而OC=3,
∴点P到x轴的距离为1,即P点的纵坐标为1,
当y=1时,x2-2x-3=1,解得x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$,则P点坐标为(1+$\sqrt{5}$,1)或(1-$\sqrt{5}$,1),
∴m=1+$\sqrt{5}$或m=1-$\sqrt{5}$,
综上所述,m的值为1或1+$\sqrt{5}$或1-$\sqrt{5}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求一次函数和二次函数的解析式;理解坐标与图形的性质;会运用分类讨论的思想解决数学问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
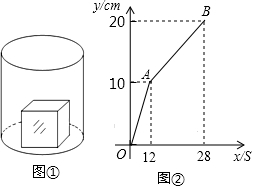 如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25的平方根是5 | B. | (-3)2的平方根是-3 | ||
| C. | $\frac{9}{25}$的算术平方根是$\frac{3}{5}$ | D. | 0.16的算术平方根是±0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CD=2CE.
如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CD=2CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
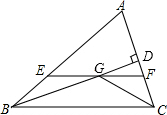 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
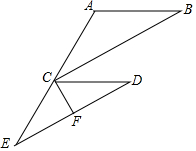 如图,AB∥CD,点E在AC上,CB平分∠ACD,∠B=30°,CF⊥DE,垂足为F,∠ECF=60°,.
如图,AB∥CD,点E在AC上,CB平分∠ACD,∠B=30°,CF⊥DE,垂足为F,∠ECF=60°,.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com