
分析 (1)根据算术平方根的定义得到2<$\sqrt{5}$<3,3<$\sqrt{13}$<4,即可得到a=$\sqrt{5}$-2,b=3,代入可得结果;
(2)根据算术平方根的定义得到2<$\sqrt{5}$<3,可得-3<$-\sqrt{5}$<-2,易得x=-3,y=3-$\sqrt{5}$;
(3)将a,b,x,y的值代入即可.
解答 解:(1)∵2<$\sqrt{5}$<3,3<$\sqrt{13}$<4,
∴a=$\sqrt{5}$-2,b=3,
∴(a-b)2-b(a+1)=-8,
∴(a-b)2-b(a+1)的立方根为-2;
(2∵2<$\sqrt{5}$<3,
∴-3<$-\sqrt{5}$<-2,
∴x=-3,y=3-$\sqrt{5}$;
(3)(x-a)(1-b+y)=(-3-$\sqrt{5}$+2)(1-3$+3-\sqrt{5}$)
=(-1$-\sqrt{5}$)(1-$\sqrt{5}$)
=4.
点评 本题主要考查了估算无理数的大小和多项式乘以多项式,利用算术平方根的定义估算出a,b,x,y是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
| 摸球的次数m | 300 | 400 | 500 | 800 | 1000 |
| 摸到白球的次数n | 186 | 242 | 296 | 483 | 599 |
| 摸到白球的频率$\frac{n}{m}$ | 0.620 | 0.605 | 0.592 | 0.604 | 0.599 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,点E,F在对角线BD上,若再添加一个条件,就可证出AE=CF.
如图,在正方形ABCD中,点E,F在对角线BD上,若再添加一个条件,就可证出AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
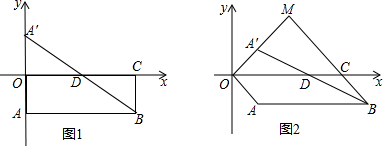
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | R1=$\frac{R{R}_{2}}{{R}_{2}-R}$ | B. | R1=$\frac{R{R}_{2}}{{R}_{2}+R}$ | C. | R1=$\frac{R{R}_{1}+R{R}_{2}}{{R}_{2}}$ | D. | R1=$\frac{R{R}_{2}}{R-{R}_{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com