
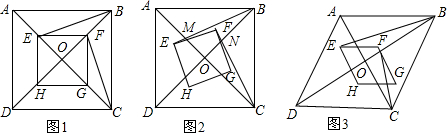
分析 (1)根据正方形的性质得到AB=CB,∠BAC=∠CBD=45°,OA=OB,OE=OD,根据线段的和差得到AE=BF,推出△ABE≌△BCF,于是得到结论;
(2)如图2,连接OE,OF,根据正方形的性质得到OE=OF,OB=OC,∠EOF=∠BOC=∠AOB=90°,由角的和差得到∠EOB=∠FOC,推出△BOE≌△COF,即可得到结论;
(3)如图3,连接OE,OF,由菱形的性质得到∠EOF=∠AOB=∠BOC=90°,根据角的和差证得∠EOB=∠FOC,由菱形的性质得到∠FEO=∠OBC=30°,于是得到tan∠FEO=$\frac{OE}{OF}$=$\frac{\sqrt{3}}{3}$,tan∠OBC=$\frac{OC}{OB}$=$\frac{\sqrt{3}}{3}$,求得$\frac{OF}{OE}=\frac{OC}{OB}$,推出△BOE∽△COF,即可得到$\frac{CF}{BE}$的值,当∠ABC=∠FEH=α,由菱形的性质得到∠FEO=∠OBC=$\frac{1}{2}α$,根据三角函数正切的定义即可得到结论.
解答 解:(1)∵四边形ABCD与四边形EFGH是正方形,
∴AB=CB,∠BAC=∠CBD=45°,OA=OB,OE=OD,
∴AE=BF,
在△ABE与△CBF中,$\left\{\begin{array}{l}{AB=BC}\\{∠BAC=∠CBD}\\{AE=BF}\end{array}\right.$,
∴△ABE≌△BCF,
∴BE=CF;
(2)如图2,连接OE,OF,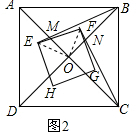
∵四边形ABCD与四边形EFGH是正方形,
∴OE=OF,OB=OC,∠EOF=∠BOC=∠AOB=90°,
∴∠EOM=∠FON,
∴∠EOB=∠FOC,
在△BEO与△COF中$\left\{\begin{array}{l}{OE=OF}\\{∠BOE=∠COF}\\{OB=OC}\end{array}\right.$,
∴△BOE≌△COF,
∴BE=CF;
(3)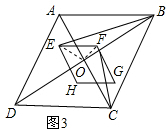 如图3,连接OE,OF,
如图3,连接OE,OF,
∵四边形ABCD与四边形EFGH是菱形,
∴∠EOF=∠AOB=∠BOC=90°,
∴∠EOA=∠FOB,
∴∠EOB=∠FOC,
∵∠ABC=∠FEH=60°,
∴∠FEO=∠OBC=30°,
∴tan∠FEO=$\frac{OE}{OF}$=$\frac{\sqrt{3}}{3}$,tan∠OBC=$\frac{OC}{OB}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{OF}{OE}=\frac{OC}{OB}$,
∴△BOE∽△COF,
∴$\frac{CF}{BE}=\frac{OF}{OE}$=$\frac{\sqrt{3}}{3}$;
当∠ABC=∠FEH=α,
∴∠FEO=∠OBC=$\frac{1}{2}α$,
∴$\frac{CF}{BE}=\frac{OF}{OE}$=tan$\frac{1}{2}α$.
点评 本题考查了正方形的性质,菱形的性质,相似三角形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
 若计算器的四个键的序号如图所示,在角的度量单位为“度的状态下”用计算器求sin47°,正确的按键顺序是( )
若计算器的四个键的序号如图所示,在角的度量单位为“度的状态下”用计算器求sin47°,正确的按键顺序是( )| A. | (1)(2)(3)(4) | B. | (2)(4)(1)(3) | C. | (1)(4)(2)(3) | D. | (2)(1)(4)(3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直径为6的半圆绕直径AB的端点A顺时针旋转45°,点B的对应点为B′,则图中阴影部分的面积是( )
如图,直径为6的半圆绕直径AB的端点A顺时针旋转45°,点B的对应点为B′,则图中阴影部分的面积是( )| A. | $\frac{3}{4}π$ | B. | $\frac{9}{4}π$ | C. | $\frac{9}{2}π$ | D. | 9π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com