
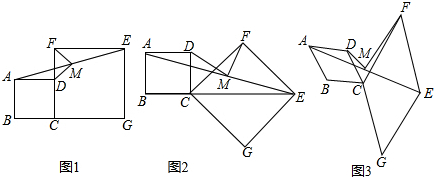
分析 (1)延长DM交EF于点P,易证AM=EM,即可证明△ADM≌△EPM,可得DM=PM,根据△DFP是直角三角形即可解题;
(2)延长DM交CE于点N,连接FN、DF,易证∠DAM=∠NEM,即可证明△ADM≌△ENM,可得EN=AD,DM=MN,可证CD=EN,即可证明△CDF≌△ENF,可得DF=NF,即可解题.
(3)根据(1)(2)的解答,可知$\frac{MD}{MF}$=tanα.
解答 证明:(1)MD=MF,MD⊥MF,如图1,延长DM交EF于点P,
∵四边形ABCD和四边形FCGE是正方形,
∴AD∥EF,∠MAD=∠MEP.∠CFE=90°.
∴△DFP是直角三角形.
∵M为AE的中点,
∴AM=EM.
在△ADM和△EPM中,
$\left\{\begin{array}{l}{∠MAD=∠MEP}\\{AM=EM}\\{∠AMD=∠EMP}\end{array}\right.$,
∴△ADM≌△EPM(ASA),
∴DM=PM,AD=PE,
∴M是DP的中点.
∴MF=$\frac{1}{2}$DP=MD,
∵AD=CD,
∴CD=PE,
∵FC=FE,
∴FD=FP,
∴△DFP是等腰直角三角形,
∴FM⊥DP,
即FM⊥DM.
(2)MD=MF,MD⊥MF,
如图2,延长DM交CE于点N,连接FN、DF,
∵CE是正方形CFEG对角线,
∴∠FCN=∠CEF=45°,
∵∠DCE=90°,
∴∠DCF=45°,
∵AD∥BC,
∴∠DAM=∠NEM,
在△ADM和△ENM中,
$\left\{\begin{array}{l}{∠DAM=∠NEM}\\{AM=EM}\\{∠AMD=∠EMN}\end{array}\right.$,
∴△ADM≌△ENM(ASA),
∴EN=AD,DM=MN,
∵AD=CD,
∴CD=EN,
在△CDF和△ENF中,
$\left\{\begin{array}{l}{CD=EN}\\{∠DCF=∠CEF=4{5}^{°}}\\{CF=EF}\end{array}\right.$,
∴△CDF≌△ENF,(SAS)
∴DF=NF,
∴FM=DM,FM⊥DM.
(3)根据(1)(2)的解答,可知$\frac{MD}{MF}$=tanα.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADM≌△ENM和△CDF≌△ENF是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=6.以D为直角顶点CD为腰向外作等腰Rt△CDE,连接AE,则△ADE的面积是4.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=6.以D为直角顶点CD为腰向外作等腰Rt△CDE,连接AE,则△ADE的面积是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
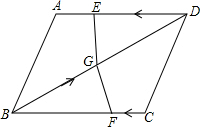 如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=12,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C,作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=12,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C,作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的顶点都在坐标轴上,OA=2,OC=3,OB=4.点E,F分别是线段AB,BC上的动点(不与端点A,B重合),点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动,同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动(当点E停止时,点F也同时停止),当两个动点运动了t秒时,解答下列问题:
如图,在平面直角坐标系中,△ABC的顶点都在坐标轴上,OA=2,OC=3,OB=4.点E,F分别是线段AB,BC上的动点(不与端点A,B重合),点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动,同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动(当点E停止时,点F也同时停止),当两个动点运动了t秒时,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是( )| A. | -4<x<1 | B. | x<-3或x>1 | C. | x<-4或x>1 | D. | -3<x<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com