
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
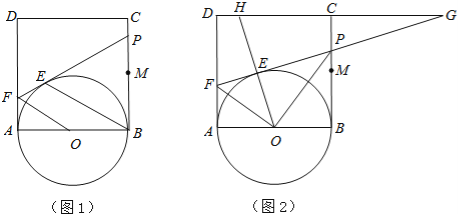
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC与H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
【答案】(1)首先证明Rt△FAO≌Rt△FEO进而得出∠AOF=∠ABE,即可得出答案。
(2)(1<x<2)。
(3)存在这样的P点。理由见解析。
【解析】
分析:(1)首先证明Rt△FAO≌Rt△FEO进而得出∠AOF=∠ABE,即可得出答案。
(2)过F作FQ⊥BC于Q,利用勾股定理求出y与x之间的函数关系,根据M是BC中点以及BC=2,即可得出BP的取值范围。
(3)首先得出当∠EFO=∠EHG=2∠EOF时,即∠EOF=30°时,Rt△EFO∽Rt△EHG,求出y=AF=OAtan30°=![]() ,即可得出答案。
,即可得出答案。
解:(1)证明:连接OE,
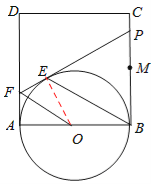
∵FE、FA是⊙O的两条切线,∴∠FAO=∠FEO=90°。
在Rt△OAF和Rt△OEF中,∵![]() ,
,
∴Rt△FAO≌Rt△FEO(HL)。
∴∠AOF=∠EOF=![]() ∠AOE。∴∠AOF=∠ABE。
∠AOE。∴∠AOF=∠ABE。
∴OF∥BE。
(2)过F作FQ⊥BC于Q,
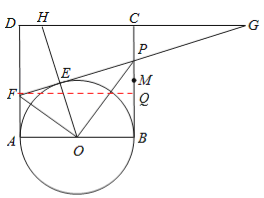
∴PQ=BP﹣BQ=x﹣y,
PF=EF+EP=FA+BP=x+y。
∵在Rt△PFQ中,FQ2+QP2=PF2,
∴22+(x﹣y)2=(x+y)2
化简得:![]() (1<x<2)。
(1<x<2)。
(3)存在这样的P点。理由如下:
∵∠EOF=∠AOF,
∴∠EHG=∠EOA=2∠EOF。
当∠EFO=∠EHG=2∠EOF时,即∠EOF=30°时,Rt△EFO∽Rt△EHG,
此时Rt△AFO中,y=AF=OAtan30°=![]() ,
,
∴![]() 。
。
∴当![]() y=
y=![]() ,时,△EFO∽△EHG。
,时,△EFO∽△EHG。


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
2016年人均阅读16本书!
2017年4月23日“世界读书日”之前,国际网络电商亚马逊发布了“亚马逊中国2017全民阅读报告”.报告显示,大部分读者已养成一定的阅读习惯,阅读总量在10本以上的占56%,而去年阅读总量在10本以上的占48%.
京东图书也发布了2016年度图书阅读报告.根据京东图书文娱业务部数据统计,2016年销售纸书人均16册,总量叠在一起相当于15000个帝国大厦的高.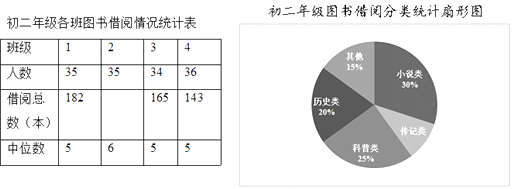
(1)在亚马逊这项调查中,以每年有效问卷1.4万份来计,2017年阅读量十本以上的人数比去年增加了人;
(2)小雨作为学校的图书管理员,根据初二年级每位同学本学期的借书记录,对各个班借阅的情况作出了统计,并绘制统计图表如下:
①全年级140名同学中有科技社团成员40名,他们人均阅读科普类书籍1.5本,年级其他同学人均阅读科普类书籍1.08本,请你计算全年级人均阅读科普类书籍的数量,再通过计算补全统计表;
②在①的条件下,若要推荐初二某个班级为本学期阅读先进集体,你会推荐哪个班,请写出你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
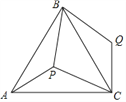
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数 ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.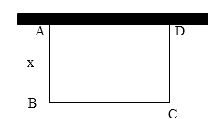
(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图ABCD是一个正方形花园,E、F是它的两个门,且DE=CF,要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?请证明你的猜想. 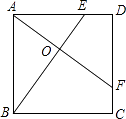
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com