
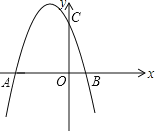
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)点P(![]() ,﹣2
,﹣2![]() )或(﹣
)或(﹣![]() ,2
,2![]() )或(﹣2+
)或(﹣2+![]() ,﹣4+2
,﹣4+2![]() )或(﹣2﹣
)或(﹣2﹣![]() ,﹣4﹣2
,﹣4﹣2![]() );(3)点F坐标(﹣2,3)或(﹣1+
);(3)点F坐标(﹣2,3)或(﹣1+![]() ,﹣3)或(﹣1﹣
,﹣3)或(﹣1﹣![]() ,﹣3)
,﹣3)
【解析】
(1)由待定系数法可求解析式;
(2)求出点C坐标,可得OA=OC=3,由面积关系列出方程可求解;
(3)分两种情况讨论,利用平行四边形的性质可求解.
解:(1)∵抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,
∴![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=﹣x2﹣2x+3;
(2)∵抛物线y=﹣x2﹣2x+3与y轴交于点C,
∴点C(0,3)
∴OA=OC=3,
设点P(x,﹣x2﹣2x+3)
∵S△PAO=2S△PCO,
∴![]() ×3×|﹣x2﹣2x+3|=2×
×3×|﹣x2﹣2x+3|=2×![]() ×3×|x|,
×3×|x|,
∴x=±![]() 或x=﹣2±
或x=﹣2±![]() ,
,
∴点P(![]() ,﹣2
,﹣2![]() )或(﹣
)或(﹣![]() ,2
,2![]() )或(﹣2+
)或(﹣2+![]() ,﹣4+2
,﹣4+2![]() )或(﹣2﹣
)或(﹣2﹣![]() ,﹣4﹣2
,﹣4﹣2![]() );
);
(3)若BC为边,且四边形BCFE是平行四边形,
∴CF∥BE,
∴点F与点C纵坐标相等,
∴3=﹣x2﹣2x+3,
∴x1=﹣2,x2=0,
∴点F(﹣2,3)
若BC为边,且四边形BCEF是平行四边形,
∴BE与CF互相平分,
∵BE中点纵坐标为0,且点C纵坐标为3,
∴点F的纵坐标为﹣3,
∴﹣3=﹣x2﹣2x+3
∴x=﹣1±![]() ,
,
∴点F(﹣1+![]() ,﹣3)或(﹣1﹣
,﹣3)或(﹣1﹣![]() ,﹣3);
,﹣3);
若BC为对角线,则四边形BECF是平行四边形,
∴BC与EF互相平分,
∵BC中点纵坐标为![]() ,且点E的纵坐标为0,
,且点E的纵坐标为0,
∴点F的纵坐标为3,
∴点F(﹣2,3),
综上所述,点F坐标(﹣2,3)或(﹣1+![]() ,﹣3)或(﹣1﹣
,﹣3)或(﹣1﹣![]() ,﹣3).
,﹣3).


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在综合与实践课上,同学们以“三角形的折叠”为主题开展数学活动.
操作发现
“杨辉”小组的同学用一张钝角三角形纸片![]() ,
,![]() 为钝角,进行了如下操作:
为钝角,进行了如下操作:
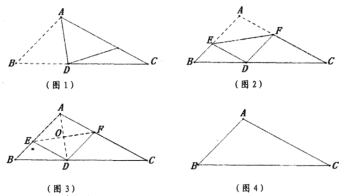
第一步:如图1,折出![]() 的角平分线
的角平分线![]() ;
;
第二步:如图2,展平纸片,再次折叠该三角形纸片,使预点![]() 与点
与点![]() 重合,拆痕
重合,拆痕![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ;
;
第三步:如图3,再次展平纸片,连接![]() ,
,![]() ,可得四边形
,可得四边形![]() .
.
(1)在图4的![]() 中利用尺规作出折痕
中利用尺规作出折痕![]() ,
,![]() ;
;
(要求:保留作图痕迹,不写作法)
实践探究
(2)试判断图3中四边形![]() 的形状,并写出证明过程;
的形状,并写出证明过程;
深入探究
(3)“陈景润”小组的同学突发奇想,在“杨辉”小组同学操作的基础上设计了这样一个问题:在图3中,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,利用相似三角形的知识可以求出
,利用相似三角形的知识可以求出![]() 的长.请你写出求解过程.
的长.请你写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:

若n=24,则第2019次“F”运算的结果是( )
A.4B.1C.2018D.42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AB=5,BC=8,点P为BC上一动点(不与端点重合),连接AP,将△ABP沿着AP折叠.点B落到M处,连接BM、CM,若△BMC为等腰三角形,则BP的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实疫情期间的垃圾分类,树立全面环保意识,某校举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了不完整的两种统计图:
四个等级,并绘制了不完整的两种统计图:
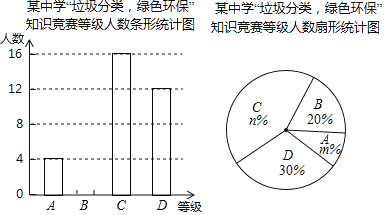
根据图中提供的信息,回答下列问题:
(1)参加知识竞赛的学生共有______人,并把条形统计图补充完整;
(2)扇形统计图中,![]() ______,
______,![]() ______,
______,![]() 等级对应的圆心角为______度;
等级对应的圆心角为______度;
(3)小明是四名获![]() 等级的学生中的一位,学校将从获
等级的学生中的一位,学校将从获![]() 等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
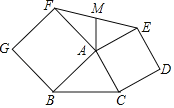
【题目】已知:如图,在△ABC中,cos∠ABC=![]() ,sin∠ACB=
,sin∠ACB=![]() ,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则△AEF的面积为_____,AM的长为_____.
,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则△AEF的面积为_____,AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌电脑销售公司有营销员14人,销售部为制定营销人员月销售电脑定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
人数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)该公司营销员销售该品牌电脑的月销售平均数是 台,中位数是 台,众数是 台.
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com