
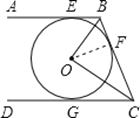
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
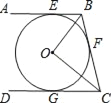
【答案】(1)∠BOC=90°;(2)BE+CG =10cm;(3)OF=4.8cm.
【解析】试题分析:(1)连接OF,根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;再根据平行线性质得到∠BOC为直角;
(2)进而由切线长定理即可得到BE+CG的长;
(3)由勾股定理可求得BC的长,最后由三角形面积公式即可求得OF的长.
试题解析:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°;
(2)∵OB=6cm,OC=8cm,
∴BC=10cm,
∴BE+CG=BC=10cm.
(3)OF=4.8


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】为切实做好校园疫情防控和开学的各项准备工作,某校准备再次购进免手洗消毒凝胶和医用口罩用于防疫,若购进30箱医用口罩和20箱免手洗消毒凝胶共需8500元;若购进40箱医用口罩和10箱免手洗消毒凝胶共需8000元.
(1)求医用口罩和免手洗消毒凝胶每箱购进价格分别为多少元?
(2)若该校购进免手洗消毒凝胶的数量比购进医用口罩数量的2倍少10箱,且用于购置两种物资的总经费不超过9000元,则该校至多购进医用口罩多少箱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=2
,EF=2![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上。
(1)如果点P在C、D之间运动时,试说明∠1+∠3=∠2;
(2)如果点P在直线l1的上方运动时,试探索∠1,∠2,∠3之间的关系又是如何?
(3)如果点P在直线l2的下方运动时,试探索∠PAC,∠PBD,∠APB之间的关系又是如何? (直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
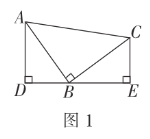
【题目】(1)如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() .
.
(2)如图2,已知点![]() ,点
,点![]() ,
,![]() ,
,![]() ,且点
,且点![]() 在第一象限,求
在第一象限,求![]() 所在直线的表达式.
所在直线的表达式.
(3)如图3,在长方形![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在
上的动点且在![]() 轴的右侧.若
轴的右侧.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请求出点
为直角顶点的等腰直角三角形,请求出点![]() 的坐标.
的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
把代数式通过配凑等手段得到局部完全平方式,再进行有关计算和解题,这种解题方法叫做配方法.
如(1)用配方法分解因式:![]() .
.
解:原式=![]()
=![]()
(2)M=![]() ,利用配方法求M的最小值.
,利用配方法求M的最小值.
解:M=![]()
=![]()
![]()
![]() M有最小值1.
M有最小值1.
请根据上述材料,解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:![]()
(2)用配方法分解因式:![]()
(3)若M=![]() ,求M的最小值.
,求M的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
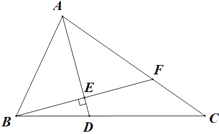
【题目】如图,在△ABC中,∠ABC=65°,∠C=35°,AD是△ABC的角平分线.
(1)求∠ADC的度数.
(2)过点B作BE⊥AD于点E,BE延长线交AC于点F.求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(![]() ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y=![]() 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是_____.
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形平移与旋转”为主题开展数学活动,![]() 和
和![]() 是两个等边三角形纸片,其中,
是两个等边三角形纸片,其中,![]() .
.
解决问题
(1)勤奋小组将![]() 和
和![]() 按图1所示的方式摆放(点
按图1所示的方式摆放(点![]() 在同一条直线上) ,连接
在同一条直线上) ,连接![]() .发现
.发现![]() ,请你给予证明;
,请你给予证明;

(2)如图2,创新小组在勤奋小组的基础上继续探究,将![]() 绕着点
绕着点![]() 逆时针方向旋转,当点
逆时针方向旋转,当点![]() 恰好落在
恰好落在![]() 边上时,求
边上时,求![]() 的面积;
的面积;

拓展延伸
(3)如图3,缜密小组在创新小组的基础上,提出一个问题: “将![]() 沿
沿![]() 方向平移
方向平移![]() 得到
得到![]() 连接
连接![]() ,当
,当![]() 恰好是以
恰好是以![]() 为斜边的直角三角形时,求
为斜边的直角三角形时,求![]() 的值.请你直接写出
的值.请你直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com