
����Ŀ���Ķ����ϣ����ǰѶ�����Բ�ϣ�����һ�ߺ�Բ�ཻ����һ�ߺ�Բ���еĽǽ������нǣ���ͼ1��ABC��ʾ��ͬѧ���о����֣�PΪԲ������һ�㣬����AC����Բ��Oʱ����AB�С�O�ڵ�A����ʱ���нǡ�CAB=��P��ͼ2��
֤������AB�С�O�ڵ�A�����CAB=90�㣬�֡�AC��ֱ�������P=90����CAB=��P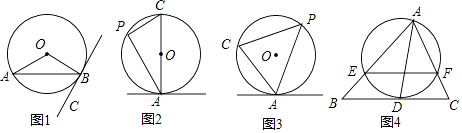
������չ����AC������Բ��O����ͼ3�����ý��ۣ����нǡ�CAB=��P����������˵�����ɣ�
֪ʶ���ã���ͼ4��AD�ǡ�ABC�С�BAC��ƽ���ߣ�������A�ġ�O��BC���ڵ�D����AB��AC�ֱ��ཻ��E��F����֤��EF��BC��
���𰸡��⣺������չ��������
��ͼ3������AO���ӳ�����O�ڵ�D������CD��
���D=��P��
��AD��ֱ����
���D+��CAD=90�㣬
�֡�AB��Բ�ڵ�A��
���CAB+��CAD=90�㣬
���CAB=��CAD��
����CAD=��P��
���CAB=��P��
֪ʶ���ã���ͼ4������DF��
��AD�ǡ�ABC�С�BAC��ƽ���ߣ�
���EAD=��DAC��
�ߡ�O��BC���ڵ�D��
���FDC=��DAC��
���FDC=��EAD��
���ڡ�O�С�EAD=��EFD��
���FDC=��EFD��
��EF��BC��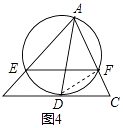
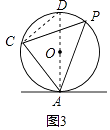
��������������չ����������AO���ӳ�����O�ڵ�D������CD����Բ�ܽǶ����ɵá�D=��P������AD��ֱ����AB��Բ�ڵ�A����֤�á�CAB=��CAD���̶�֤�ý��ۣ�
֪ʶ���ã�����DF��AD�ǡ�ABC�С�BAC��ƽ���ߣ���O��BC���ڵ�D���ɵá�FDC=��EAD������Բ�ܽǶ����ɵá�EAD=��EFD���̶�֤�ý��ۣ�
�����㾫����������Ĺؼ������������ߵ����ʶ��������֪ʶ���������ߵ����ʣ�1�������е㴹ֱ�������뾶��ֱ����Բ������2�������е㴹ֱ�����ߵ�ֱ�߱ؾ���Բ��3��Բ�����ߴ�ֱ�ھ����е�İ뾶��


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ���㣨��1��0������5��0������0����5����
��1����˶��κ����Ľ���ʽ��
��2����0��x��5ʱ����˺�������Сֵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���C=90�㣬AC=BC=4cm��D��AB���е㣬��CΪԲ�ģ�4cm��Ϊ�뾶��Բ����A��B��C��D�ĵ��У���Բ�ڵ��У� ��
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC���������Σ�����CDEF�������������εĽ����ߡ������� ![]() ��
�� ![]() ��
�� ![]() Բ�����ΰ�A��B��C��ѭ�����������������ӣ���AB=1��������CDEF��������������У���
Բ�����ΰ�A��B��C��ѭ�����������������ӣ���AB=1��������CDEF��������������У��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�պϵ�·�У������˵�ѹ�㶨������I��A�������R������ͼ����ͼ��ʾ���ش����⣺ 
��1��д������I�����R֮��ĺ�������ʽ��
��2�����һ���õ����ĵ���Ϊ5����������ͨ������������1A����ô����õ�����������պϵ�·�У�����ջ٣�˵�����ɣ�
��3���������ĵ���������4Aʱ����ô����R��ȡֵӦ�ÿ�����ʲô��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AB��AC��BD��CD�ֱ�ƽ�֡�ABC�͡�ACB.�ʣ�(����ʱ��ע����д����)
(1)ͼ�����м������������Σ�(д����������Ҫ֤��)
(2)��D����EF��BC����AB��E����AC��F����ͼ�ڣ�ͼ�������˼������������Σ�ѡһ������֤����
(3)��ͼ�ۣ��������е���ABC��Ϊ���ȱ������Σ������������䣬ͼ���м������������Σ��߶�EF��BE��CF��ʲô��ϵ��(д����������Ҫ֤��)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺(![]() )��2��
)��2��![]() +��
+��![]() ��4��0��
��4��0��![]() cos45�㣮
cos45�㣮
���𰸡�1
�������������������ԭʽ�ĵ�һ����ݸ�����ָ���ݵ����廯�ڶ����������ƽ�����Ķ������9������ƽ�����������������ָ����ʽ�������һ����������ǵ����Ǻ���ֵ���ϲ������ֵ.
���������ԭʽ=4��3+1��![]()
=2��1
=1��
�����͡������
��������
16
����Ŀ��������������������������һ�⣺�����ж���ͬ�������������ߣ������������Ҷ��У�������ʮ����б�������һᣮ�ʼ����и���������������˵����֪�ס��Ҷ���ͬʱ��ͬһ��
����������ٶ�Ϊ7���ҵ��ٶ�Ϊ3����һֱ���ߣ�����������10��������б��ƫ����������һ�κ�������������ô����ʱ�������Ҹ����˶�Զ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ı���ABCD��AD��BC��AB=4��BC=6��CD=5��AD=3.
���ı���ABCD�����.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com