Question

（本题满分12分）

如图，已知抛物线y=x²+bx－3a过点A（1，0），B（0，－3），与x轴交于另一点C.

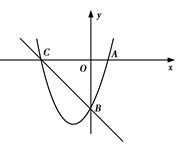
（1）求抛物线的解析式；

（2）若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，求点P的坐标；

（3）在（2）的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由.

 

Answer 1

【答案】

（1）抛物线的解析式为y=x2+2x－3 （2）点坐标为（－1，－4）（3）点Q的坐标为（－2，－3）

【解析】

试题分析：解：（1）把A（1，0），B（0，－3）代入y=x²+bx－3a中，得

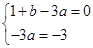
解得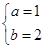

∴抛物线的解析式y=x²+2x－3

（2）令y=0，得x²+2x－3=0，

解得x₁=－3，x₂=1

∴点C（－3，0）

∵B（0，－3）

∴△BOC为等腰直角三角形.

∴∠CBO=45°过点P作PD⊥y轴，垂足为D，

∵PB⊥BC，∴∠PBD=45°∴PD=BD

所以可设点P（x，－3+x）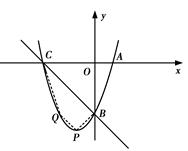

则有－3+x=x²+2x－3，∴x=－1，所以P点坐标为（－1，－4）

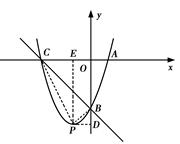
（3）由（2）知，BC⊥BP

当BP为直角梯形一底时，由图象可知点Q不可能在抛物线上.

若BC为直角梯形一底，BP为直角梯形腰时，

∵B（0，－3），C（－3，0），

∴直线BC的解析式为y=－x－3

∵直线PQ∥BC，且P（－1，－4），

∴直线PQ的解析式为y=－（x+1）－3－1即y=－x－5            

联立方程组得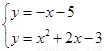

解得x₁=－1，x₂=－2

∴x=－2，y=－3，即点Q（－2，－3）

∴符合条件的点Q的坐标为（－2，－3）

考点：二次函数

点评：本题难度较大。主要考查学生对几种函数的综合运用。是中考的常考题型，复习备考时应加强训练。