

分析 (1)点B作BE⊥AC于点E,在直角三角形AEB中,利用锐角三角函数定义求出AE的长,在直角三角形CEB中,利用锐角三角函数定义求出BE与CE的长;
(2)由AE+CE求出AC的长,即可求出CD的长.
解答  解:(1)过点B作BE⊥AC于点E,
解:(1)过点B作BE⊥AC于点E,
在Rt△AEB中,AB=60m,sinA=$\frac{1}{2}$,BE=ABsinA=60×$\frac{1}{2}$=30,cosA=$\frac{AE}{AB}$,
∴AE=60×$\frac{\sqrt{3}}{2}$=30$\sqrt{3}$m,
在Rt△CEB中,∠ACB=∠CBD-∠A=75°-30°=45°,
∴BE=CE=30m;
(2)∵AE=30$\sqrt{3}$,CE=30m,
∴AC=AE+CE=(30+30$\sqrt{3}$)m,
在Rt△ADC中,sinA=$\frac{CD}{AC}$,
∴CD=(30+30$\sqrt{3}$)×$\frac{1}{2}$=(15+15$\sqrt{3}$)m.
点评 此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
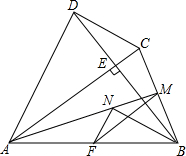 如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.试说明:
如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.试说明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BC是某塔AB在阳光下的影子(将AB,BC看成线段).
如图,BC是某塔AB在阳光下的影子(将AB,BC看成线段).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D是BC边上的一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.求证:AD是△ABC的中线.
如图,在△ABC中,D是BC边上的一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.求证:AD是△ABC的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{41}{9}$ | B. | $\frac{41}{8}$ | C. | $\frac{41}{6}$ | D. | $\frac{41}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com