
【题目】一张长方形桌子可坐6人,按图3将桌子拼在一起.

(1)2张桌子拼在一起可坐 人,4张桌子拼在一起可坐 人,n张桌子拼在一起可坐 人;
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④![]() .上述结论中正确的是( )
.上述结论中正确的是( )
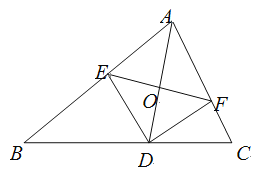
A. ②③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为(单位:环):
甲:8,8,7,8,9
乙:5,9,7,10,9
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 8 | b | 8 | 0.4 |
乙 | α | 9 | c | 3.2 |
根据以上信息,请解答下面的问题:
(1)α= ,b= ,c= ;
(2)完成图中表示乙成绩变化情况的折线;
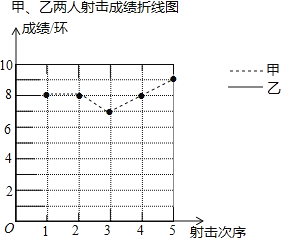
(3)教练根据这5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(4)若选手乙再射击第6次,命中的成绩是8环,则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会 .(填“变大”、“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在纸面上有一条数轴.
![]()
操作一:
(1)折叠纸面,使表示1的点与表示![]() 的点重合,则表示
的点重合,则表示![]() 的点与表示______的点重合.
的点与表示______的点重合.
操作二:
(2)折叠纸面,使表示![]() 的点与表示3的点重合,回答下列问题:
的点与表示3的点重合,回答下列问题:
①表示5的点与表示______的点重合;
②若数轴上A,B两点之间的距离为9(A在B的左侧),且折叠后A,B两点重合,求A,B两点表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“迎新年,做守法好公民”的知识竞赛中,每班参加比赛的人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将某年级的1班和2班的成绩整理并绘制成如下的统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将某年级的1班和2班的成绩整理并绘制成如下的统计图:
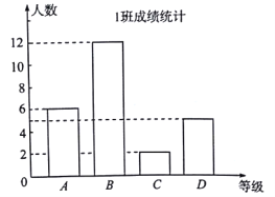

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中,2班成绩在![]() 级以上(包括
级以上(包括![]() 级)的人数为____人;
级)的人数为____人;
(2)请你将表格补充完整:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
1班 | 90 | ||
2班 | 87.6 | 100 |
(3)请从下列不同角度对这次竞赛成绩的结果进行分析;
①从平均数和中位数的角度来比较1班和2班的分成绩;
②从平均数和众数的角度来比较1班和2班的成绩;
③从![]() 级以上(包括
级以上(包括![]() 级)的人数的角度来比较1班和2班的成绩.
级)的人数的角度来比较1班和2班的成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
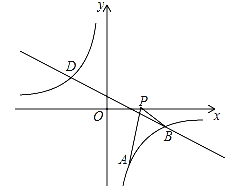
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一张边长为8的正方形纸片![]() ,点
,点![]() 为
为![]() 边上的一点(不与点
边上的一点(不与点![]() 、点
、点![]() 重合),将正方形纸片折叠,使点
重合),将正方形纸片折叠,使点![]() 落在
落在![]() 处,点
处,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于
于![]() ,折痕为
,折痕为![]() ,连结
,连结![]() 、
、![]() .
.
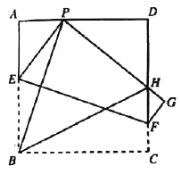
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.
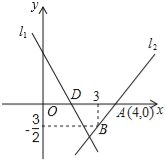
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在l2上存在异于点C的另一点P,使得△ADP与△ADC面积相等,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com