练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．在实数$\sqrt{3}$，-2，0，$-\sqrt{2}$中，最大值是（　　）
    A．$\sqrt{3}$B．-2C．0D．$-\sqrt{2}$

    分析 根据正实数大于0，负实数小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．

    解答 解：实数$\sqrt{3}$，-2，0，$-\sqrt{2}$中，最大值是$\sqrt{3}$；
    故选A．

    点评 此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．下列说法正确的是（　　）
    A．两直线被第三条直线相截，同位角相等
    B．相等的角是对顶角
    C．同旁内角互补，两直线平行
    D．互补的两个角一定有一个锐角

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．（1）计算：（2a-2b2）2•3a5b-5
    （2）解方程：$\frac{3}{x-2}$-$\frac{x}{2-x}$=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．已知直线l过A（2，0），且与直线y=2x+3平行，则直线l的解析式为y=2x-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．一次函数y=$\frac{1}{2}$x+2与y=-2x-3交于点C，则C点坐标为（-2，1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知△ABC是等腰直角三角形，AB=AC，D为平面内的任意一点，且满足CD=AC，若△ADB是以AD为腰的等腰三角形，则∠CDB的度数为45°或135°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：
    （1）18-（-2）×（-1）3-32÷（-4）2；
    （2）$\frac{7}{9}$÷（$\frac{2}{3}$-$\frac{1}{5}$）+$\frac{1}{3}$×（-3）2；
    （3）36×$（0.25-\frac{1}{9}）-{2}^{3}÷\frac{4}{9}×（-\frac{1}{3}）^{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．用两种不同的方法解下列方程：x2-4x=12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

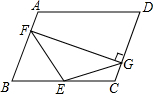    20．如图，?ABCD中，∠B=70°，点E是BC的中点，且BF=BE，过点F作FG⊥CD于点G，有如下结论：①EF=EG；②∠EFG=35°；③CE=DG；④∠FEG=100°；⑤∠EGC=55°，则正确的结论是①②⑤．（填序号即可）

    查看答案和解析>>

    同步练习册答案