
【题目】如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G,则△CEF的面积 . 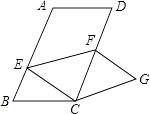
【答案】![]()
【解析】解:如图1,作CK⊥AB于K,过E点作EP⊥BC于P. 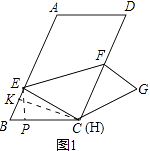
∵∠B=60°,
∴CK=BCsin60°=4× ![]() =2
=2 ![]() ,
,
∵C到AB的距离和E到CD的距离都是平行线AB、CD间的距离,
∴点E到CD的距离是2 ![]() ,
,
∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠A=∠BCD,
由折叠可知,AD=CG,∠D=∠G,∠A=∠ECG,
∴BC=GC,∠B=∠G,∠BCD=∠ECG,
∴∠BCE=∠GCF,
在△BCE和△GCF中,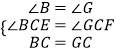 ,
,
∴△BCE≌△GCF(ASA);
∴CE=CF,
∵∠B=60°,∠EPB=90°,
∴∠BEP=30°,
∴BE=2BP,
设BP=m,则BE=2m,
∴EP=BEsin60°=2m× ![]() =
= ![]() m,
m,
由折叠可知,AE=CE,
∵AB=6,
∴AE=CE=6﹣2m,
∵BC=4,
∴PC=4﹣m,
在Rt△ECP中,由勾股定理得(4﹣m)2+( ![]() ﹣m)2=(6﹣2m)2 , 解得m=
﹣m)2=(6﹣2m)2 , 解得m= ![]() ,
,
∴EC=6﹣2m=6﹣2× ![]() =
= ![]() ,
,
∴CF=EC= ![]() ,
,
∴S△CEF= ![]() ×
× ![]() ×2
×2 ![]() =
= ![]() ,
,
故答案为 ![]() .
.
如图1,作CK⊥AB于K,过E点作EP⊥BC于P.想办法求出CK、EP、EC,再证明△BCE≌△GCF(ASA)推出CE=CF,根据三角形的面积公式计算即可.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;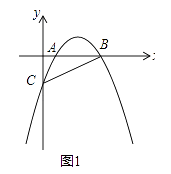
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;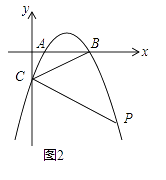
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 ![]() a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.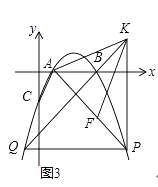
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒.请问当t为何值时,以P、Q、C为顶点的三角形是等腰三角形?
(3)若点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M、N、C、E为顶点四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
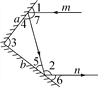
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=________,∠3=________;
(2)在(1)中,若∠1=55°,则∠3=________;若∠1=40°,则∠3=________;
(3)由(1)、(2)请你猜想:当两平面镜a,b的夹角∠3=________时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC. 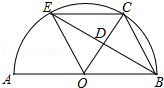
(1)求证:△BDO≌△EDC.
(2)若OB=6,则四边形OBCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
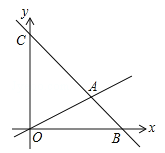
【题目】如图,在平面直角坐标系中,直线![]() 与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求点B和点C的坐标.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标,若不存在,说明理由.
?若存在,求出此时点M的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需要资金6000元;若购进3部甲型手机和2部乙型手机,共需要资金4600元.
(1) 求甲、乙型号手机每部进价为多少元?
(2) 为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com