
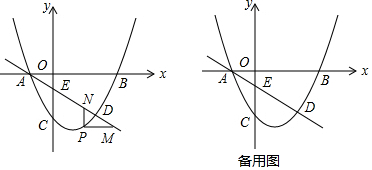
���� ��1����B��3��0����C��0��-2������y=$\frac{2}{3}$x2+bx+c�ⷽ���鼴�ɵõ����ۣ�
��2����P��m��$\frac{2}{3}$m2-$\frac{4}{3}$m-2�����õ�N��m��-$\frac{2}{3}$m-$\frac{2}{3}$����M��-m2+2m+2��$\frac{2}{3}$m2-$\frac{4}{3}$m-2�������ݶ��κ��������ʼ��ɵõ����ۣ�
��3�����E��0��-$\frac{2}{3}$�����õ�CE=$\frac{4}{3}$����P��m��$\frac{2}{3}$m2-$\frac{4}{3}$m-2��������CEΪ�ߣ�����CE=PF���з��̵õ�m=1��m=0����ȥ��������CEΪ�Խ��ߣ�����PF��CE��G��CG=GE��PG=FG���õ�G��0��-$\frac{4}{3}$������P��m��$\frac{2}{3}$m2-$\frac{4}{3}$m-2������F��-m��$\frac{2}{3}$m-$\frac{2}{3}$�����з��̵õ��˷�����ʵ���������ǵõ����ۣ�
��� �⣺��1����B��3��0����C��0��-2������y=$\frac{2}{3}$x2+bx+c�ã�$\left\{\begin{array}{l}{\frac{2}{3}��{3}^{2}+3b+c=0}\\{c=-2}\end{array}\right.$��
��$\left\{\begin{array}{l}{b=-\frac{4}{3}}\\{c=-2}\end{array}\right.$
�������ߵĽ���ʽΪ��y=$\frac{2}{3}$x2-$\frac{4}{3}$x-2��
��2����P��m��$\frac{2}{3}$m2-$\frac{4}{3}$m-2����
��PM��x�ᣬPN��y�ᣬM��N��ֱ��AD�ϣ�
��N��m��-$\frac{2}{3}$m-$\frac{2}{3}$����M��-m2+2m+2��$\frac{2}{3}$m2-$\frac{4}{3}$m-2����
��PM+PN=-m2+2m+2-m-$\frac{2}{3}$m-$\frac{2}{3}$-$\frac{2}{3}$m2+$\frac{4}{3}$m+2=-$\frac{5}{3}$m2+$\frac{5}{3}$m+$\frac{10}{3}$=-$\frac{5}{3}$��m-$\frac{1}{2}$��2+$\frac{15}{4}$��
�൱m=$\frac{1}{2}$ʱ��PM+PN�����ֵ��$\frac{15}{4}$��
��3���ܣ�
���ɣ���y=-$\frac{2}{3}$x-$\frac{2}{3}$��y���ڵ�E��
��E��0��-$\frac{2}{3}$����
��CE=$\frac{4}{3}$��
��P��m��$\frac{2}{3}$m2-$\frac{4}{3}$m-2����
����E��C��P��FΪ������ı����ܹ���ƽ���ı��Σ�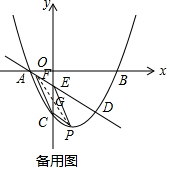
����CEΪ�ߣ���CE��PF��CE=PF��
��F��m��-$\frac{2}{3}$m-$\frac{2}{3}$����
��-$\frac{2}{3}$m-$\frac{2}{3}$-$\frac{2}{3}$m2+$\frac{4}{3}$m+2=$\frac{4}{3}$����$\frac{2}{3}$m2-$\frac{4}{3}$m-2+$\frac{2}{3}$m+$\frac{2}{3}$=$\frac{4}{3}$��
��m1=1��m2=0����ȥ����m3=$\frac{1+\sqrt{17}}{2}$��m4=$\frac{1-\sqrt{17}}{2}$��
����CEΪ�Խ��ߣ�����PF��CE��G��
��CG=GE��PG=FG��
��G��0��-$\frac{4}{3}$����
��P��m��$\frac{2}{3}$m2-$\frac{4}{3}$m-2������F��-m��$\frac{2}{3}$m-$\frac{2}{3}$����
��$\frac{1}{2}$����$\frac{2}{3}$m2-$\frac{4}{3}$m-2+$\frac{2}{3}$m-$\frac{2}{3}$��=-$\frac{4}{3}$��
��m=1��m=0����ȥ����
����������F��1��-$\frac{4}{3}$������$\frac{1+\sqrt{17}}{2}$��-$\frac{\sqrt{17}}{3}$������$\frac{1-\sqrt{17}}{2}$��$\frac{\sqrt{17}}{3}$������-1��0����E��C��P��FΪ������ı����ܹ���ƽ���ı��Σ�
���� ���⿼���˴���ϵ���������Ľ���ʽ��ƽ���ı��ε����ʣ����κ��������ʣ���ȷ�����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
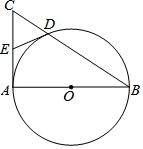 ��ͼ����Rt��ABC�У���CAB=90�㣬��ABΪֱ���ġ�O��BC�ڵ�D����E��AC���е㣬����DE��
��ͼ����Rt��ABC�У���CAB=90�㣬��ABΪֱ���ġ�O��BC�ڵ�D����E��AC���е㣬����DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij���Թ�˾����A��B��C�����ͺŵļ�Ʒ�Ƶ��Ժ�D��E�����ͺŵ���Ʒ�Ƶ��ԣ�ϣ����ѧҪ�Ӽס�������Ʒ�Ƶ����и�ѡ��һ���ͺŵĵ��ԣ�
ij���Թ�˾����A��B��C�����ͺŵļ�Ʒ�Ƶ��Ժ�D��E�����ͺŵ���Ʒ�Ƶ��ԣ�ϣ����ѧҪ�Ӽס�������Ʒ�Ƶ����и�ѡ��һ���ͺŵĵ��ԣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
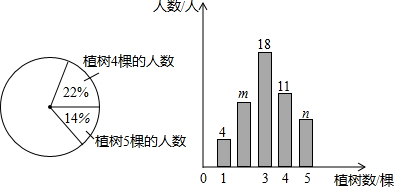
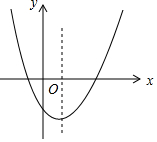 ��ͼ���Ƕ��κ���y=ax2+bx+c��ͼ�����н��ۣ���ab��0����abc��0����$\frac{4ac}{{b}^{2}}$��1�����д���ĸ����ǣ�������
��ͼ���Ƕ��κ���y=ax2+bx+c��ͼ�����н��ۣ���ab��0����abc��0����$\frac{4ac}{{b}^{2}}$��1�����д���ĸ����ǣ�������| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com