
分析 x=$\frac{\sqrt{29}-3}{2}$,即2x+3=$\sqrt{29}$,两边平方即可得到x2=5-3x,然后代入所求的代数式进行降次,则所求的代数式即可利用x表示出来,然后代入求值即可.
解答 解:∵x=$\frac{\sqrt{29}-3}{2}$,
∴2x+3=$\sqrt{29}$,
∴(2x+3)2=29,即4x2+12x-20=0,x2+3x-5=0.
∴x2=5-3x,
∴x4+5x3-3x2-8x+9=(5-3x)2+5x(5-3x)-3(5-3x)-8x+9
=25-30x+9x2+25x-15x2-15+9x-8x+9
=-6x2-4x+19
=-6(5-3x)-4x+19
=-30+18x-4x+19
=14x-11
=7($\sqrt{29}$-3)-11
=7$\sqrt{29}$-32.
故答案是:7$\sqrt{29}$-32
点评 本题考查二次根式的化简求值,对所求的代数式进行降次,利用x的一次方表示出所求的代数式是本题的关键.


科目:初中数学 来源: 题型:解答题
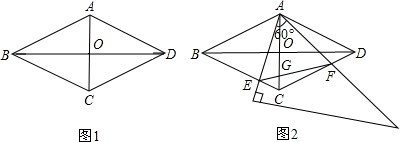
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
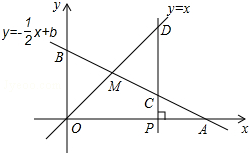 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个函数图象都经过第四象限 | |
| B. | 两个函数图象有两个公共点 | |
| C. | 两个函数在自变量的取值范围内y都随x的增大而增大 | |
| D. | 在第二象限内,函数y=x+1的值小于函数y=-$\frac{1}{x}$的值 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
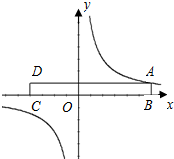 如图,将一张长方形的纸片ABCD沿x轴摆放,顶点A(6,1)恰好落在某双曲线上.现在AD边上找一点E,使得将纸片的右半部分沿OE所在直线折叠后,点A恰好还落在此双曲线上,则满足条件的点E的坐标为(1,1)(-1,1).
如图,将一张长方形的纸片ABCD沿x轴摆放,顶点A(6,1)恰好落在某双曲线上.现在AD边上找一点E,使得将纸片的右半部分沿OE所在直线折叠后,点A恰好还落在此双曲线上,则满足条件的点E的坐标为(1,1)(-1,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环跳动,即第一次跳动到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…如此下去.
如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环跳动,即第一次跳动到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…如此下去.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
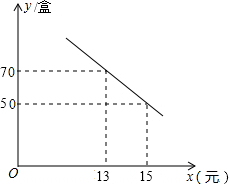 某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价x(单位:元)与每日销售量y(单位:盆)之间的函数关系如图所示.
某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价x(单位:元)与每日销售量y(单位:盆)之间的函数关系如图所示. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com