
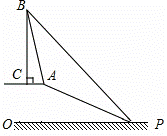
已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
据2014年1月24日某报道,某县2013年财政收入突破18亿元,在某省各县中排名第二. 将18亿用科学记数法表示为
A. 1.8×10 B. 1.8×108 C. 1.8×109 D. 1.8×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
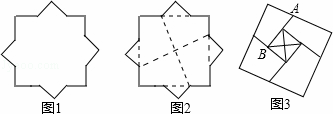
图1是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成图3所示的大正方形,其面积为8+4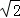 ,则图3中线段AB的长为 .
,则图3中线段AB的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
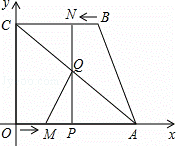
如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两班参加植树造林,已知甲班每天比乙班每天多植5棵树,甲班植80棵树所用的天数与乙班植70棵树所用的天数相等,若设甲班每天植x棵,根据题意列出的方程是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
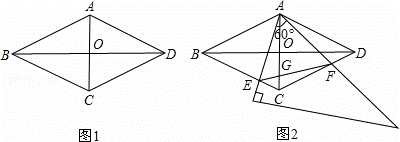
如图1,在菱形ABCD中,AC=2,BD=2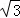 ,AC,BD相交于点O.
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com