
【题目】(知识回顾)
七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.
(理解应用)
(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,试求m的值;
(2)若一次函数y=2kx+1﹣4k的图象经过某个定点,则该定点坐标为 ;
(能力提升)
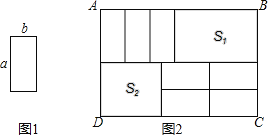
(3)7张如图1的小长方形,长为a,宽为b.按照图2方式不重叠地放在大矩形ABCD内,大矩形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变.求a与b的等量关系.
【答案】(1)m=![]() ;(2)(2,1);(3)a=2b.
;(2)(2,1);(3)a=2b.
【解析】
(1)由题可知代数式的值与x的取值无关,所以含x项的系数为0,故将多项式整理为(2m﹣3)x﹣3m+2m2,令x系数为0,即可求出m.
(2)根据题意可知图象经过某个定点即x取某定值时,函数值与k无关,故可将x作系数,把k看出字母合并同类项,原函数解析式可化为即y=2k(x﹣2)+1,当x﹣2=0时即看求出y值,即定点为(2,1).
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),即可得到S1﹣S2关于x的代数式,根据取值与x可得a=2b.
解:(1)(2x﹣3)m+2m2﹣3x=2mx﹣3m+2m2﹣3x=(2m﹣3)x﹣3m+2m2,
∵若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,
∴2m﹣3=0,
∴m=![]() .
.
(2)∵y=2kx+1﹣4k=2k(x﹣2)+1,
当x=2时,y=1,故一次函数y=2kx+1﹣4k的图象经过定点(2,1),
故答案为:(2,1)
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2=a(x﹣3b)﹣2b(x﹣2a)=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变.
∴S1﹣S2取值与x无关,
∴a﹣2b=0
∴a=2b.


科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦AC为6cm,
(1)用尺规作图画出∠ACB的平分线交⊙O于点D.(不要写作法,保留作图痕迹)
(2)分别连接点AD和BD,求弦BC、AD、BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.

(1)观察图形,写出图中所有与∠AED相等的角.
(2)选择图中与∠AED相等的任意一个角,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的引桥部分的示意图,梯面AD、BE相互平行,且与地面成37°的夹角,DE是一段水平歇台,离地面高度3米.已知天桥高度BC为4.8米,引桥水平跨度AC为8米,求梯面AD、BE及歇台DE的长.(参考数据:![]() ,结果保留两位小数)
,结果保留两位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
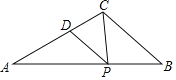
【题目】如图,在△ABC中,AB=6,AC=4,∠A=30°,线段AB上有一个动点P,过点P作PD∥BC,交AC于D,连接PC,则△PCD的最大面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE
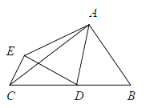
(1)求证:AD=ED
(2)连接BE,猜想△BEC的形状,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=![]() ,则PB+PC=_____.
,则PB+PC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
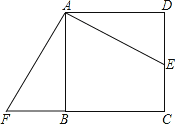
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com