
【题目】如图,□ABCD中,AB=6,E是BC边的中点,F为CD边上一点,DF=4.8,∠DFA=2∠BAE,则AF 的长为( )
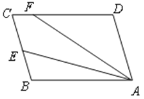
A. 4.8B. 6C. 7.2D. 10.8
【答案】C
【解析】
在AF上截取AG=AB,连接EG,CG.利用全等三角形的判定定理SAS证得△AEG≌△AEB,由全等三角形的对应角相等、对应边相等知EG=BE,∠B=∠AGE;然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得CF=FG;最后根据线段间的和差关系证得结论.
在AF上截取AG=AB,连接EG,CG.
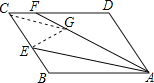
∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=6,
∴∠DFA=∠BAF,
∵∠DFA=2∠BAE,
∴∠FAE=∠BAE,
在△BAE和△GAE中,
 ,
,
∴△BAE≌△GAE(SAS).
∴EG=BE,∠B=∠AGE;
又∵E为BC中点,
∴CE=BE.
∴EG=EC,
∴∠EGC=∠ECG;
∵AB∥CD,
∴∠B+∠BCD=180°.
又∵∠AGE+∠EGF=180°,∠AGE=∠B,
∴∠BCF=∠EGF;
又∵∠EGC=∠ECG,
∴∠FGC=∠FCG,
∴FG=FC;
∵DF=4.8,
∴CF=CD-DF=6-4.8=1.2,
又∵AG=AB,
∴AF=AG+GF=AB+FC=CD+FC=6+1.2=7.2.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
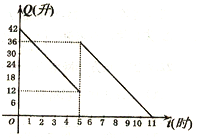
【题目】某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图,回答下列问题(1)机动车行驶________小时后加油,中途加油_______升;(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并直接写出自变量t的取值范围;(3)如果加油站距目的地还有230千米,车速为40千米/时,要到达目的地,油箱中的油是否够用?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
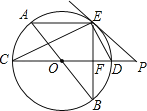
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c所表示的数在数轴上的位置如图所示:
![]()
(1)化简:│a-1│-│c+b│+│b-1│;
(2)若a+b+c=0,且b与-1的距离和c与-1的距离相等,求:-a2+2b-c-(a-4c-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数:
0,3,8,15,24,…①
2,5,10,17,26,…②
0,6,16,30,48,…③
(1)第①行数按什么规律排的,请写出来?
(2)第②、③行数与第①行数分别对比有什么关系?
(3)取每行的第![]() 个数,求这三个数的和.
个数,求这三个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电话拨号上网有两种收费方式,用户可以任选其一:
![]() :计时制:0. 03元/分.
:计时制:0. 03元/分. ![]() :38元/月(限一部个人住宅电话上网).
:38元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0. 01元/分. 某用户某月上网时间为![]() 小时,
小时,
(1)若按照![]() 方式收费为_____元(用含
方式收费为_____元(用含![]() 的代数式表示),若按照
的代数式表示),若按照![]() 方式收费为_____元(用含
方式收费为_____元(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() 小时,通过计算采用哪种方式较为合算?
小时,通过计算采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
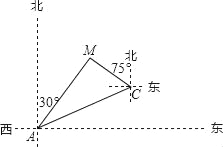
【题目】如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达C处,测得小区M位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,并求AN的长.(精确到1米,![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
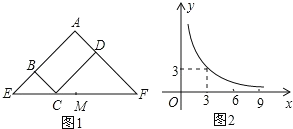
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的序号是___.①当x=3时,EC<EM;②当y=9时,EC>EM③当x增大时,ECCF的值增大;④当y增大时,BEDF的值不变。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com