
【题目】“学而时习之,不亦乐乎!”,古人把经常复习当作是一种乐趣,能达到这种境界是非常不容易的.复习可以让遗忘的知识得到补拾,零散的知识变得系统,薄弱的知识有所强化,掌握的知识更加巩固,生疏的技能得到训练.为了了解初一学生每周的复习情况,教务处对初一(1)班学生一周复习的时间进行了调查,复习时间四舍五入后只有4种:1小时,2小时,3小时,4小时,一周复习2小时的女生人数占全班人数的16%,一周复习4小时的男女生人数相等.根据调查结果,制作了两幅不完整的统计图(表):

分组(四舍五入后) | 频数(学生人数) |
1小时 | 2 |
2小时 | a |
3小时 | 4 |
4小时 | b |
初一(1)班女生的复习时间数据(单位:小时)如下:0.9,1.3,1.7,1.8,1.9,2.2,2.2,2.2,2.3,2.4,3.2,3.2,3.2,3.3,3.8,3.9,3.9,4.1,4.2,4.3.
女生一周复习时间频数分布表
(1)四舍五入前,女生一周复习时间的众数为______小时,中位数为______小时;
(2)统计图表中a=______,c=______,初一(1)班男生人数为______人,根据扇形统计图估算初一(1)班男生一周的平均复习时间为______小时;
(3)为了激励学生养成良好的复习习惯,教务处决定对一周复习时间四舍五入后达到3小时及以上的全年级学生进行表扬,每人奖励1个笔记本,初一年级共有1000名学生,请问教务处应该准备大约多少个笔记本?
【答案】(1)2.2、3.2,2.8(2)8,20,2.5(3)教务处应该准备大约440个笔记本
【解析】
(1)根据出现次数最多找到众数,根据偶数个数的中位数的计算方法计算中位数即可;
(2)先数出复习两小时的女生人数,再计算该班人数和男生人数.由复习四小时的男女人数相等,得到d,再计算出c,利用加权平均数计算男生一周的平均复习时间;
(3)先计算初一(1)班复习时间3小时以上人数占全班的比例,利用该数据估计教务处应该买的笔记本数.
(1)2.2与3.2出现的次数都是3次,都是出现次数最多的数;![]() =2.8.
=2.8.
故答案为:2.2、3.2,2.8
(2)初一(1)班一周复习2小时的女生人数共8人,即a=8;
因为一周复习2小时的女生人数占全班人数的16%,
所以该班人数为:8÷16%=50(人)
因为该班有女生20人,所以有男生50-20=30(人).
一周复习4小时的女生有:b=20-2-8-4=6(人)
因为该班一周复习4小时的男女生人数相等.
所以一周复习4小时的男生占男生人数的百分比为:![]() =20%,即d=20,
=20%,即d=20,
所以c=100-10-50-20=20.
所以男生一周的平均复习时间为:2×50%+1×10%+4×20%+3×20%=2.5(小时)
故答案为:8,20,2.5
(3)初一(1)班复习时间在三小时及以上的人数有:4+6+6+30×20%=22(人)
占该班人数的![]() =44%,
=44%,
教务处该准备笔记本:1000×44%=440(个)
答:教务处应该准备大约440个笔记本


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将抛物线y1=x2﹣2x﹣3先向左平移1个单位,再向上平移4个单位后,与抛物线y2=ax2+bx+c重合,现有一直线y3=2x+3与抛物线y2=ax2+bx+c相交.当y2≤y3时自变量x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=![]() ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,
,![]() ,且点B在双曲线
,且点B在双曲线![]() 上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且
上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且![]() ,则线段CE长度的取值范围是
,则线段CE长度的取值范围是![]()
![]()
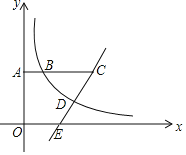
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABO中,∠B=90°,∠OAB=30°,OA=3.以点O为原点,斜边OA所在直线为x轴,建立平面直角坐标系,以点P(4,0)为圆心,PA长为半径画圆,⊙P与x轴的另一交点为N,点M在⊙P上,且满足∠MPN=60°.⊙P以每秒1个单位长度的速度沿x轴向左运动,设运动时间为ts,解答下列问题:
(发现)(1)![]() 的长度为多少;
的长度为多少;
(2)当t=2s时,求扇形MPN(阴影部分)与Rt△ABO重叠部分的面积.
(探究)当⊙P和△ABO的边所在的直线相切时,求点P的坐标.
(拓展)当![]() 与Rt△ABO的边有两个交点时,请你直接写出t的取值范围.
与Rt△ABO的边有两个交点时,请你直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() 与x轴交于A,B(点A在点B的左侧)与y轴交于点C,连接AC、BC.过点A作AD∥BC交抛物线于点D(8
与x轴交于A,B(点A在点B的左侧)与y轴交于点C,连接AC、BC.过点A作AD∥BC交抛物线于点D(8![]() ,10),点P为线段BC下方抛物线上的任意一点,过点P作PE∥y轴交线段AD于点E.
,10),点P为线段BC下方抛物线上的任意一点,过点P作PE∥y轴交线段AD于点E.
(1)如图1.当PE+AE最大时,分别取线段AE,AC上动点G,H,使GH=5,若点M为GH的中点,点N为线段CB上一动点,连接EN、MN,求EN+MN的最小值;
(2)如图2,点F在线段AD上,且AF:DF=7:3,连接CF,点Q,R分别是PE与线段CF,BC的交点,以RQ为边,在RQ的右侧作矩形RQTS,其中RS=2,作∠ACB的角平分线CK交AD于点K,将△ACK绕点C顺时针旋转75°得到△A′CK′,当矩形RQTS与△A′CK′重叠部分(面积不为0)为轴对称图形时,请直接写出点P横坐标的取值范围.
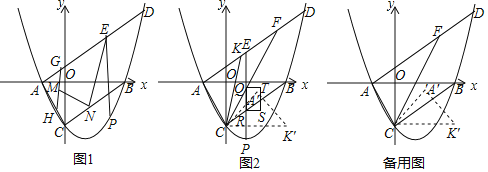
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
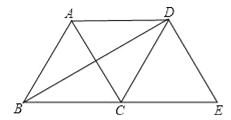
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com