
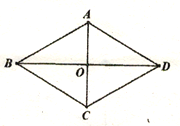
【题目】已知在菱形ABCD中,对角线AC、BD交于点O,AB=2AO;(1)如图1,求∠BAC的度数;(2)如图2,P为菱形ABCD外一点,连接AP、BP、CP,若∠CPB=120°,求证:CP+BP=AP;(3)如图3,M为菱形ABCD外一点,连接AM、CM、DM,若∠AMD=150°,
CM=2![]() ,DM=2,求四边形ACDM的面积。
,DM=2,求四边形ACDM的面积。
【答案】(1)∠BAC=60°;(2)见解析;(3)![]() .
.
【解析】
(1)如图1中,证明△ABC是等边三角形即可解决问题.
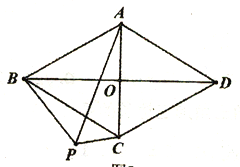
(2)在PA上截取PH,使得PH=PC,连接CH.证明△PCB≌△HCA(SAS)即可;
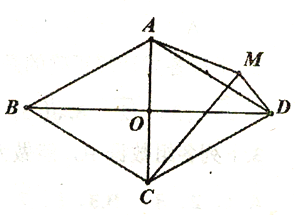
(3)如图3中,作AH⊥DM交DM的延长线于H,延长AC到N,使得CN=AC,连接DN.证明A,N,D,M四点共圆,外接圆的圆心是点C,推出AD=CM=![]() ,解直角三角形求出AH即可解决问题.
,解直角三角形求出AH即可解决问题.
解:(1)如图1中,
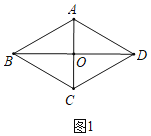
∵四边形ABCD是菱形,
∴AC⊥BD,∠ABD=∠CBD,
∴∠AOB=90°,
∵AB=2OA,
∴∠ABO=30°,
∴∠ABC=60°,
∵BA=BC,
∴△ABC是等边三角形,
∴∠BAC=60°;
(2)证明:如图2中,

在PA上截取PH,使得PH=PC,连接CH.
∵∠BPC=120°,∠BAC=60°,
∴∠BPC+∠BAC=180°,
∴A,B,P,C四点共圆,
∴∠APC=∠ABC=60°,
∵PH=PC,
∴△PCH是等边三角形,
∴PC=CH,∠PCH=∠ACB=60°,
∴∠PCB=∠HCA,
∵CB=CA,CP=CH,
∴△PCB≌△HCA(SAS),
∴PB=AH,
∴PA=PH+AH=PC+PB;
(3)解:如图3中,作AH⊥DM交DM的延长线于H,延长AC到N,使得CN=AC,连接DN.
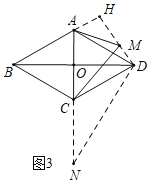
∵CA=CD=CN,
∴∠ADN=90°,
∵CD=CN,
∴∠N=∠CDN,
∵∠ACD=60°=∠N+∠CDN,
∴∠N=30°,
∵∠AMD=150°,
∴∠N+∠AMD=180°,
∴A,N,D,M四点共圆,外接圆的圆心是点C,
∴CA=CD=AD=CM=![]() ,
,
在Rt△AHM中,∵∠AMH=30°,
∴MH=![]() AH,设AH=x,则HM=
AH,设AH=x,则HM=![]() x,
x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴28=x2+(![]() x+2)2,
x+2)2,
解得x=![]() 或-2
或-2![]() (舍弃),
(舍弃),
∴AH=![]() ,
,
∴S四边形ACDM=S△ACD+S△ADM=![]() ×
×![]() +
+![]() ×2×
×2×![]() =
=![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() ,求
,求![]() 的度数. (提示:作
的度数. (提示:作![]() ).
).
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,求
,求![]() 与
与![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点![]() 在射线
在射线![]() 上运动,请你直接写出
上运动,请你直接写出![]() 与
与![]() 、
、![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题(1)、(2)
解方程:|x+3|=2.
当x+30时,原方程可化为:x+3=2,解得x=1;
当x+3<0时,原方程可化为:x+3=2,解得x=5.
所以原方程的解是x=1,x=5.
(1)解方程:|3x1|5=0;
(2)探究:当b为何值时,方程|x2|=b+1①无解;②只有一个解;③有两个解.
查看答案和解析>>
科目:初中数学 来源: 题型:
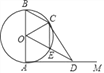
【题目】如图,AB是圆O的直径,射线AM⊥AB,点D在AM上,连接OD交圆O于点E,过点D作DC=DA交圆O于点C(A、C不重合),连接OC、BC、CE.
(1)求证:CD是⊙O的切线;
(2)若圆O的直径等于2,填空:
①当AD= 时,四边形OADC是正方形;
②当AD= 时,四边形OECB是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
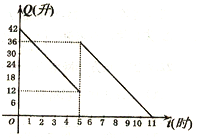
【题目】某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图,回答下列问题(1)机动车行驶________小时后加油,中途加油_______升;(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并直接写出自变量t的取值范围;(3)如果加油站距目的地还有230千米,车速为40千米/时,要到达目的地,油箱中的油是否够用?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足![]() =AD,连接CE并延长交AD于点F,连接AE,过点B作
=AD,连接CE并延长交AD于点F,连接AE,过点B作![]() 于点G,延长BG交AD于点H.在下列结论中:①
于点G,延长BG交AD于点H.在下列结论中:①![]() ;②
;②![]() ;③
;③![]() . 其中不正确的结论有( )
. 其中不正确的结论有( )
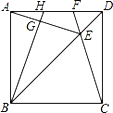
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
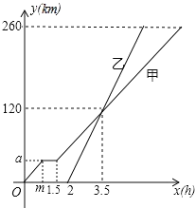
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)直接写出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x (h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车出发多长时间后,两车恰好相距40km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电话拨号上网有两种收费方式,用户可以任选其一:
![]() :计时制:0. 03元/分.
:计时制:0. 03元/分. ![]() :38元/月(限一部个人住宅电话上网).
:38元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0. 01元/分. 某用户某月上网时间为![]() 小时,
小时,
(1)若按照![]() 方式收费为_____元(用含
方式收费为_____元(用含![]() 的代数式表示),若按照
的代数式表示),若按照![]() 方式收费为_____元(用含
方式收费为_____元(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() 小时,通过计算采用哪种方式较为合算?
小时,通过计算采用哪种方式较为合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com