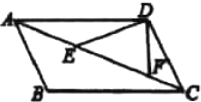
【题目】如图，在
中，
、
是对角线
上两点，
，
，
，则
的大小为______.
【答案】
【解析】
由平行四边形的性质可得∠BAD=∠BCD=66°，∠BAC=∠ACD，根据直角三角形斜边中线的性质可得AE=ED，可得∠EAD=∠ADE，根据等腰三角形的性质可得∠DCE=∠DEC，由三角形外角性质可得∠DEC=2∠ADE，即可得出∠BAD=3∠ADE，即可得答案.
∵四边形ABCD是平行四边形，∠BCD=66°，
∴∠BAD=∠BCD=66°，∠BAC=∠ACD，
∵AE=EF，∠ADF=90°，
∴AE=DE，
∴∠EAD=∠ADE，
∵AE=CD，
∴DE=CD，
∴∠DCE=∠DEC，
∵∠DEC=∠DAE+∠ADE=2∠ADE，
∴∠BAD=∠BAC+∠DAE=∠DEC+∠ADE=3∠ADE=66°，
∴∠ADE=22°.
故答案为：22°
优翼小帮手同步口算系列答案科目：初中数学 来源： 题型：
【题目】已知一次函数
和反比例函数
．
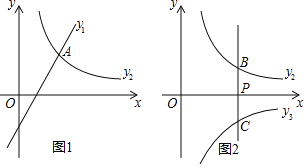
（1）如图1，若
，且函数
、
的图象都经过点
．
①求
，
的值；
②直接写出当
时
的范围；
（2）如图2，过点
作
轴的平行线
与函数的图象相交于点
，与反比例函数
的图象相交于点
．
①若
，直线与函数的图象相交点
．当点、、中的一点到另外两点的距离相等时，求
的值；
②过点作轴的平行线与函数的图象相交于点
．当的值取不大于1的任意实数时，点、间的距离与点、间的距离之和
始终是一个定值．求此时的值及定值．
查看答案和解析>>
科目：初中数学 来源： 题型：
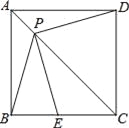
【题目】如图，P是正方形ABCD对角线AC上一点，点E在BC上，且PE=PB．
（1）求证：PE=PD；
（2）连接DE，试判断∠PED的度数，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图象与反比例函数
(
且
)的图象在第一象限交于点
、
，且该一次函数的图象与
轴正半轴交于点
，过、分别作轴的垂线，垂足分别为
、
．已知
，
．
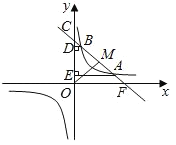
(1)求
的值和反比例函数的解析式；
(2)若点
为一次函数图象上的动点，求
长度的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
的顶点坐标为
，经过点
.
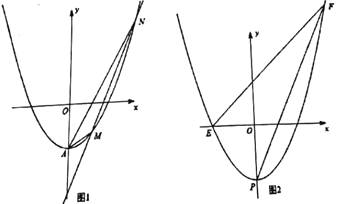
（1）求抛物线的解析式；
（2）如图1，直线
交抛物线于
，
两点，若
，求
的值；
（3）如图2，将抛物线向下平移
个单位长度得到抛物线
，抛物线的顶点为
，交
轴的负半轴于点
，点
在抛物线上.
①求点的坐标（用含
的式子表示）；
②若
，求，
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，斜边AC的中点M关于BC的对称点O，将△ABC绕点O顺时针旋转至△DCE，连接BD，BE，如图所示.
(1)在①
，②
，③
中，等于旋转角的是 （填出满足条件的角的序号）；
(2)若
求
的大小（用含
的式子表示）；
(3)点N是BD的中点，连接MN，用等式表示线段MN与BE之间的数量关系，并证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知P为正方形ABCD外的一点，PA=1，PB=2，将△ABP绕点B顺时针旋转90°，使点P旋转至点P′，且AP′=3，则∠BP′C的度数为 （ ）
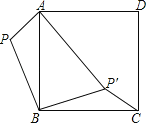
A．105° B．112.5° C．120° D．135°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】近几年，移动电商发展迅速，以下是2017年某调查机构发布的相关的统计表和统计图的一部分。请根据以上信息解答下列问题：
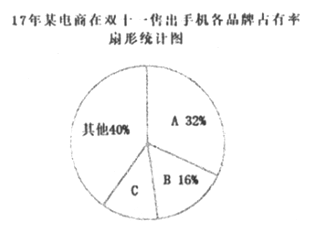
（1）2017年10月“移动电商行业用户规模”是___________亿台（结果精确到0.1亿台）；并补全条形统计图；
（2）2017年10—12这三个月“移动电商行业用户规模”比上个月增长台数的平均数为___________亿台，若按此平均数增长，请你估计2018年1月“移动电商行业用户规模”为___________亿台（结果精确到0.1亿台）；
（3）2017年某电商在双十一共售出手机12000台，则C品牌手机售出的台数是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
