
【小题1】已知 ,当
,当 时,求
时,求 的值。
的值。
【小题2】解方程组
科目:初中数学 来源: 题型:
 ,即
,即 ,有下面的不等式:
,有下面的不等式: 当且仅当
当且仅当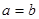 时取到等号
时取到等号 叫做正数
叫做正数 的算术平均数,把
的算术平均数,把 叫做正数
叫做正数 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子: ,求函数
,求函数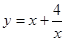 的最小值。
的最小值。 ,则有
,则有 ,得
,得 ,当且仅当
,当且仅当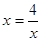 时,即
时,即 时,函数有最小值,最小值为
时,函数有最小值,最小值为 。
。 ,则当
,则当 时,函数
时,函数 取到最小值,最小值
取到最小值,最小值 的矩形花园,问这个矩形的长、宽各为多少时,所
的矩形花园,问这个矩形的长、宽各为多少时,所 ,则自变量
,则自变量 取何值时,函数
取何值时,函数 取到最大值,最大值为多少?
取到最大值,最大值为多少?查看答案和解析>>
科目:初中数学 来源:2012届天津市红桥区中考二模数学试卷(带解析) 题型:解答题
已知一抛物线经过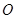 (0,0),
(0,0), (1,1)两点,且解析式的二次项系数为
(1,1)两点,且解析式的二次项系数为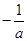
( >0).
>0).
【小题1】当 时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
【小题2】已知点 (0,1),若抛物线与射线
(0,1),若抛物线与射线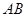 相交于点
相交于点 ,与
,与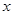 轴相交于点
轴相交于点 (异于原点),当
(异于原点),当 在什么范围内取值时,
在什么范围内取值时,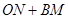 的值为常数?当
的值为常数?当 在什么范围内取值时,
在什么范围内取值时, 的值为常数?
的值为常数?
【小题3】若点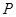 (
(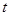 ,
,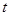 )在抛物线上,则称点
)在抛物线上,则称点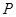 为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线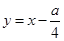 上,请说明理由.
上,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com