
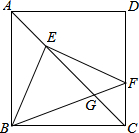
 如图,已知,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于G,则BG与GF的乘积为$3\sqrt{2}-4$.
如图,已知,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于G,则BG与GF的乘积为$3\sqrt{2}-4$. 分析 连接DE,根据等腰三角形得出∠DEF=45°,再利用三角形全等得出EF=BE,进而得出△EGF~△BGC,利用相似三角形的性质得出BG•GF=EG•GC,进而得出GC=AE=$\sqrt{2}-1$,EG=1-GC=2-$\sqrt{2}$,即可得出两者乘积.
解答 解:连接DE,如图: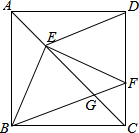
∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°,BC=DC=1,
∵EC=BC,
∴∠CBE=∠BEC=67.5°,
∵EF⊥BE,
∴∠CEF=22.5°,
∵EC=BC=DC,
∴∠DEF=45°,∠EDC=67.5°,
∴△EFD是等腰三角形,
∴ED=EF,
∵△BEC和△DEC是等腰三角形,且BC=CE=CD,
∴BE=ED,
∴BE=EF,
∴△BEF是等腰直角三角形,
∴∠GBC=∠EBC-∠EBF=67.5°-45°=22.5°=∠CEF,
∵∠EGF=∠BGC,
∴△EGF∽△BGC,
∴BG•GF=EG•GC,
∵CE=AB=CB=1,
∴AE=$\sqrt{2}-1=GC$,
∴EG=EC-GC=2-$\sqrt{2}$,
∴EG•GC=$(\sqrt{2}-1)(2-\sqrt{2})=3\sqrt{2}-4$,
∴BG•GF=$3\sqrt{2}-4$.
故答案为:$3\sqrt{2}-4$.
点评 此题考查正方形的性质,关键是利用全等三角形和相似三角形的判定和性质分析解答.


科目:初中数学 来源: 题型:解答题
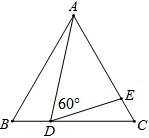 已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
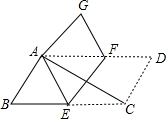 如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
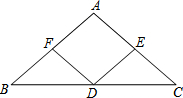 已知:如图,D是△ABC的边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE,
已知:如图,D是△ABC的边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解全国中学生每天体育锻炼的时间,应采用普查的方式 | |||||||||||||
| B. | 甲组数据的方差${S_甲}^2$=0.03,乙组数据的方差是${S_乙}^2$=0.2,则乙组数据比甲组数据稳定 | |||||||||||||
| C. | 广州市明天一定会下雨 | |||||||||||||
| D. | 某班学生数学成绩统计如下,则该班学生数学成绩的众数和中位数分别是80分,80分
|
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a-2a=a | B. | -2a(3a-1)=-6a2-1 | ||
| C. | -8a2÷2a=-4a | D. | (a+3b)2=a2+6ab+9b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com