
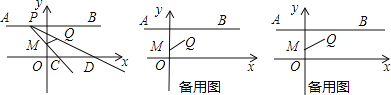
����Ŀ����֪��ͼ����ƽ��ֱ������ϵ�����ĵ㣬����ֱ�ΪA����4��3����B��4��3����M��0��1����Q��1��2��������P���߶�AB�ϣ��ӵ�A�������B��ÿ��1����λ�˶�������PM��PQ���ӳ��ֱ�x����C��D���㣨��ͼ����
��1���ڵ�P�ƶ��Ĺ����У�����M��C��D��Q��Χ���ı��Σ���t��ȡֵ��Χ��_________����д����t��2ʱ����C������______________��
��2���ڵ�P�ƶ��Ĺ����У���PMQ��������Գ�ͼ�������ܣ���������������ĵ�P�����ꣻ�����ܣ���˵�����ɣ�
��3���ڵ�P�ƶ��Ĺ����У����ı���MCDQ�����S�ķ�Χ��
���𰸡�(1)0��t��8��t��6��C��1,0��; (2)P����1,3����0,3��; (3)0��S��![]() ;
;
����������������� ![]() �����ֱ��
�����ֱ��![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() �Ļ������Ҫʹ
�Ļ������Ҫʹ![]() �ܹ����ı��Σ���ô
�ܹ����ı��Σ���ô![]() ������߶�
������߶�![]() ���˶����Ҳ���ֱ��
���˶����Ҳ���ֱ��![]() �ϣ��ɴ˿����
�ϣ��ɴ˿����![]() ��ȡֵ��Χ����
��ȡֵ��Χ����![]() ʱ��
ʱ�� ![]() ����
����![]() �ɵó�
�ɵó�![]() ��
��![]()
![]() ���
���![]() ����Գ�ͼ�Σ���ô
����Գ�ͼ�Σ���ô![]() ��Ϊ���������Σ�Ӧ����������������
��Ϊ���������Σ�Ӧ����������������![]() �㣺
�㣺
��![]() ��
��![]() �Ĵ�ֱƽ�����ϣ������
�Ĵ�ֱƽ�����ϣ������![]() ������꣬Ȼ��������ϵ�����ľ��빫ʽ��ʾ��
������꣬Ȼ��������ϵ�����ľ��빫ʽ��ʾ��![]() ��
�� ![]() ���ڴ�ʱ
���ڴ�ʱ �ݴ˿����
�ݴ˿����![]() �����ꣻ
�����ꣻ
�ڸ���![]() ��
��![]() �������֪���������
�������֪���������![]() ��ô
��ô![]() �ǵ���ֱ�������Σ����
�ǵ���ֱ�������Σ����![]() �㼴
�㼴![]() Ҳ��������������
Ҳ��������������![]() ʱ����ֱ��
ʱ����ֱ��![]() �ϣ�����һ�㣬�����ǵ���ֱ��
�ϣ�����һ�㣬�����ǵ���ֱ��![]() �ϣ���˲���������ȥ����
�ϣ���˲���������ȥ����
![]() ����ֻ�����
����ֻ�����![]() �����ֵ���ɣ�������������ۣ�
�����ֵ���ɣ�������������ۣ�
�ٵ�![]() ʱ����
ʱ����![]() ��
��![]() ����
����![]() ����ʱ�ı���
����ʱ�ı���![]() �������������
�������������![]() �����+
�����+![]() -
-![]() ��ã��ɴ˿ɵó�����
��ã��ɴ˿ɵó�����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
�ڵ�![]() ʱ���������������
ʱ���������������![]() �����+
�����+![]() +
+![]() ���.
���.
�۵�![]() ʱ�����������
ʱ�����������![]() -����
-����![]() �����-
�����-![]() ��ã�
��ã�
����������������ó��ĺ�����ϵʽ�����Ե��Ա���ȡֵ��Χ�������![]() �����ֵ�����ɵó�
�����ֵ�����ɵó�![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���������(1) ![]() ��t��6;��C������Ϊ(1,0)��
��t��6;��C������Ϊ(1,0)��

(2)����PMQ��������Գ�ͼ�Σ�����PMQ��Ϊ���������Ρ�
�ٵ�PQ=PMʱ,��P������ΪP(a,3)�����У�
![]() ��֪
��֪![]()
![]()
���a=2��a=0��
��a=2ʱ��AP=4+2=6����t=6�������⣬��ȥ.
��P������Ϊ(0,3)��
�ڵ�PM=MQʱ,��P������ΪP(b,3)�����У�
![]()
![]()
���b=1��
��P������Ϊ(1,3).
������������P������Ϊ(1��3)��(0��3)��
(3)��![]() ʱ,
ʱ, ![]()
��![]() ʱ,
ʱ, ![]()
��![]()
![]()
���ı���MCDQ�����S�ķ�Χ��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. .x3x3��xB. ��ab3��2��ab6C. x8��x4��x2D. ��2x��3��8x3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���뾶Ϊ1����λ��ԲƬ����һ��A�������ϵ�ԭ���غϣ�AB��ԲƬ��ֱ��������������У� 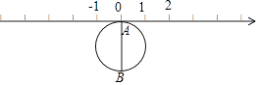
��1����ԲƬ�������������1�ܣ���A���������ϵ�C��λ�ã���C��ʾ��������������������������������������
��2����ԲƬ���������2�ܣ���A���������ϵ�D��λ�ã���D��ʾ��������
��3��ԲƬ�����������ҹ�����������Ϊ������ԲƬ�����������������������Ϊ�����������˶������¼���£�+2����1��+3����4����3 �ٵڼ��ι�����A�����ԭ��������ڼ��ι�����A�����ԭ����Զ��
�ڵ�ԲƬ�����˶�ʱ��A���˶���·�̹��ж��٣���ʱ��A����ʾ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ѧ����ҵʱ��ÿ��ͬѧ�����Լ�����Ƭ��ȫ������ͬѧ����һ�������ȫ�����2070����Ƭ����ȫ����x��ѧ�����������⣬�г�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ��4x��4����4x��5��+2y��1+3��y��2��ֵ�� ��
A.��x��y����
B.ֻ��x�й�
C.ֻ��y�й�
D.��x��y���й�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и������У���ֵ��ȵ��ǣ� ��
A.23��32
B.����2��2�ͩ�22
C.2��|��2|
D.�� ![]() ��2��
��2�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м����У������ȷ���ǣ� ��
A.��a��b��2=a2��b2
B.����2��3=8
C.![]()
D.6a2��2a2=3a2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com