
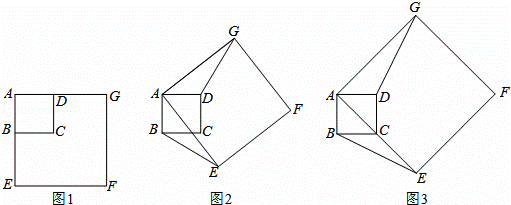
如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)当点C在直线BE上时,连接FC,直接写出∠FCD的度数;
(3)如图3,如果α=45°,AB=2,AE=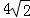 ,求点G到BE的距离.
,求点G到BE的距离.
(1)证明:如图2,
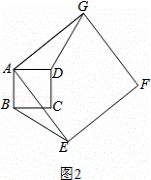
∵四边形ABCD是正方形,
∴AB=AD,∠BAE+∠EAD=90°,
又∵四边形AEFG是正方形,
∴AE=AG,∠EAD+∠DAG=90°,
∴∠BAE=∠DAG.
∴在△ABE与△ADG中,
 ,
,
∴△ABE≌△ADG(SAS),
∴BE=DG;
(2)解:①如图3,连接AC,AF,CF,

∵四边形ABCD与AEFG是正方形,
∴∠ACD=∠AFE=45°,
∵∠DCE=90°
∴点A,C,E,F四点共圆,
∵∠AEF是直角,
∴AF是直径,
∴∠ACF=90°,
∵∠ACD=45°,
∴∠FCD=45°
②如图4,连接AC,AF,FG,CG

由(1)知∵△ABE≌△ADG,
∴∠ABE=∠ADG=90°,
∴DG和CG在同一条直线上,
∴∠AGD=∠AGC=∠BAG,
∵四边形ABCD与AEFG是正方形,
∴∠BAC=∠BAE=45°,
∴∠BAG+∠GAC=45°,∠ BAG+∠BAF=45°,
BAG+∠BAF=45°,
∴∠AGD+∠GAC=45°,
∴∠BAG+∠BAF+∠AGD+∠GAC+∠AGF=180°,
∴点A,C,G,F四点共圆,
∵∠AGF是直角,
∴AF是直径,
∴∠ACF=90°,
∴∠FCD=90°+ 45°=135°.
45°=135°.
(3)解:如图5,连接GB、GE,

由已知α=45°,可知∠BAE=45°.
又∵GE为正方形AEFG的 对角线,
对角线,
∴∠AEG=45°.
∴AB∥GE.
∵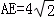 ,AB与GE间的距离相等,
,AB与GE间的距离相等,
∴GE=8, .
.
过点B作BH⊥AE于点H,
∵AB=2,
∴ .
.
∴ .
.
∴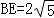 .
.
设点G到BE的距离为h.
∴ .
.
∴ .
.
即点G到BE的距离为 .
.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )

A. 16cm B.18cm C.20cm D. 22cm
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求△ABC所扫过的图形的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为 .
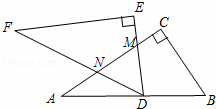
查看答案和解析>>
科目:初中数学 来源: 题型:
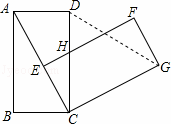
如图,在矩形ABCD中,AB=4,BC=3,将矩形绕点C按顺时针方向旋转,使点B落在线段AC上,得矩形CEFG,边CD与EF交于点H,连接DG.
(1)CH= .
(2)求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
观察图中尺规作图痕迹,下列结论错误的是( )

A. PQ为∠APB的平分线 B. PA=PB C. 点A、B到PQ的距离不相等 D. ∠APQ=∠BPQ
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E、F为圆心,大于 EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠ACD=120°,则∠MAB的度数为 .
EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠ACD=120°,则∠MAB的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,七年级(下)教材第4页给出了利用三角尺和直尺画平行线的一种方法,能说明AB∥DE的条件是( )
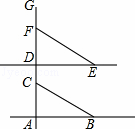
A. ∠CAB=∠FDE B.∠ACB=∠DFE C.∠ABC=∠DEF D. ∠BCD=∠EFG
查看答案和解析>>
科目:初中数学 来源: 题型:
已知下列命题:
①若a>0,b>0,则ab>0;
②直径是弦;
③若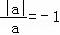 ,则a>0;
,则a>0;
④线段垂直平分线上的点到这条线段两个端点的距离相等.
其中原命题与逆命题均为真命题的个数是( )
A. 4 B.3 C.2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com