
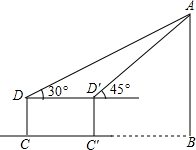
 在数学活动课中,测量组为了测量河对岸高层建筑物AB的高度,在C处用测角仪由点D测得顶端A的仰角是30°,向高层建筑前进30米到达C'处,由D'测得顶端A的仰角为45°,已知测量仪高1.1米,求建筑物AB的高.(
在数学活动课中,测量组为了测量河对岸高层建筑物AB的高度,在C处用测角仪由点D测得顶端A的仰角是30°,向高层建筑前进30米到达C'处,由D'测得顶端A的仰角为45°,已知测量仪高1.1米,求建筑物AB的高.(| 3 |
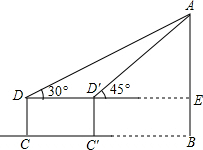 解:延长DD′交AB于E,则DE⊥AB;
解:延长DD′交AB于E,则DE⊥AB;| AE |
| DE |
| x |
| 30+x |
| 1 | ||
|
| 3 |


科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
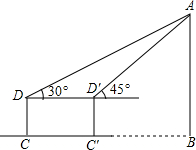 在数学活动课中,测量组为了测量河对岸高层建筑物AB的高度,在C处用测角仪由点D测得顶端A的仰角是30°,向高层建筑前进30米到达C'处,由D'测得顶端A的仰角为45°,已知测量仪高1.1米,求建筑物AB的高.(
在数学活动课中,测量组为了测量河对岸高层建筑物AB的高度,在C处用测角仪由点D测得顶端A的仰角是30°,向高层建筑前进30米到达C'处,由D'测得顶端A的仰角为45°,已知测量仪高1.1米,求建筑物AB的高.( ≈1.732结果保留2个有效数字)
≈1.732结果保留2个有效数字)查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《锐角三角函数》(05)(解析版) 题型:解答题
 ≈1.732结果保留2个有效数字)
≈1.732结果保留2个有效数字)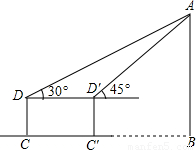
查看答案和解析>>
科目:初中数学 来源:2002年四川省广元市中考数学试卷(解析版) 题型:解答题
 ≈1.732结果保留2个有效数字)
≈1.732结果保留2个有效数字)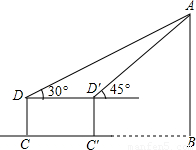
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com