
 BC,则∠BAC的度数为________°.
BC,则∠BAC的度数为________°. BC,推出AD=BD=DC,即可求出∠BAC=90°;②当AB=BC时,求出AD=
BC,推出AD=BD=DC,即可求出∠BAC=90°;②当AB=BC时,求出AD= AB,求出∠B=30°,求出∠BAC=∠C=
AB,求出∠B=30°,求出∠BAC=∠C= (180°-∠B),代入求出即可;③当AC=BC时,与②解法类似,求出∠BAC=75°.④△ABC是钝角三角形,BA=BC.
(180°-∠B),代入求出即可;③当AC=BC时,与②解法类似,求出∠BAC=75°.④△ABC是钝角三角形,BA=BC.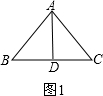
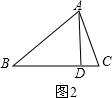
 BC,
BC, BC,
BC, BC,
BC, AB,
AB, (180°-∠B)=75°;
(180°-∠B)=75°; BC=
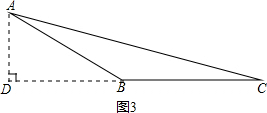
BC=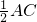 ,
,


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
 24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;
24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;查看答案和解析>>
科目:初中数学 来源: 题型:
| 120 |
| 13 |
| 120 |
| 13 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com