
”¾ĢāÄæ”æČēĶ¼£¬±ß³¤ĪŖ1µÄÕż·½ŠĪABCDµÄ¶Ō½ĒĻßAC”¢BDĻą½»ÓŚµćO£®ÓŠÖ±½Ē”ĻMPN£¬Ź¹Ö±½Ē¶„µćPÓėµćOÖŲŗĻ£¬Ö±½Ē±ßPM”¢PN·Ö±šÓėOA”¢OBÖŲŗĻ£¬Č»ŗóÄꏱÕėŠż×Ŗ”ĻMPN£¬Šż×Ŗ½ĒĪŖ¦Č£Ø0”ć£¼¦Č£¼90”ć£©£¬PM”¢PN·Ö±š½»AB”¢BCÓŚE”¢FĮ½µć£¬Į¬½ÓEF½»OBÓŚµćG£¬ŌņĻĀĮŠ½įĀŪÖŠÕżČ·µÄŹĒ £®
£Ø1£©EF=![]() OE£»£Ø2£©SĖıߊĪOEBF£ŗSÕż·½ŠĪABCD=1£ŗ4£»£Ø3£©BE+BF=
OE£»£Ø2£©SĖıߊĪOEBF£ŗSÕż·½ŠĪABCD=1£ŗ4£»£Ø3£©BE+BF=![]() OA£»£Ø4£©ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±”÷BEFÓė”÷COFµÄĆ껿֮ŗĶ×ī“óŹ±£¬AE=
OA£»£Ø4£©ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±”÷BEFÓė”÷COFµÄĆ껿֮ŗĶ×ī“óŹ±£¬AE=![]() £»£Ø5£©OGBD=AE2+CF2£®
£»£Ø5£©OGBD=AE2+CF2£®

”¾“š°ø”æ£Ø1£©£¬£Ø2£©£¬£Ø3£©£¬£Ø5£©£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©”ßĖıߊĪABCDŹĒÕż·½ŠĪ£¬
”ąOB=OC£¬”ĻOBE=”ĻOCF=45”ć£¬”ĻBOC=90”ć£¬
”ą”ĻBOF+”ĻCOF=90”ć£¬
”ß”ĻEOF=90”ć£¬
”ą”ĻBOF+”ĻCOE=90”ć£¬
”ą”ĻBOE=”ĻCOF£¬
ŌŚ”÷BOEŗĶ”÷COFÖŠ£¬
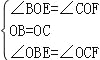 £¬
£¬
”ą”÷BOE”Õ”÷COF£ØASA£©£¬
”ąOE=OF£¬BE=CF£¬
”ąEF=![]() OE£»¹ŹÕżČ·£»
OE£»¹ŹÕżČ·£»
£Ø2£©”ßSĖıߊĪOEBF=S”÷BOE+S”÷BOE=S”÷BOE+S”÷COF=S”÷BOC=![]() SÕż·½ŠĪABCD£¬
SÕż·½ŠĪABCD£¬
”ąSĖıߊĪOEBF£ŗSÕż·½ŠĪABCD=1£ŗ4£»¹ŹÕżČ·£»
£Ø3£©”ąBE+BF=BF+CF=BC=![]() OA£»¹ŹÕżČ·£»
OA£»¹ŹÕżČ·£»
£Ø4£©¹żµćO×÷OH”ĶBC£¬
”ßBC=1£¬
”ąOH=![]() BC=
BC=![]() £¬
£¬
ÉčAE=x£¬ŌņBE=CF=1©x£¬BF=x£¬
”ąS”÷BEF+S”÷COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]() x£Ø1©x£©+
x£Ø1©x£©+![]() £Ø1©x£©”Į
£Ø1©x£©”Į![]() =©
=©![]() £Øx©
£Øx©![]() £©2+
£©2+![]() £¬
£¬
”ßa=©![]() £¼0£¬
£¼0£¬
”ąµ±x=![]() Ź±£¬S”÷BEF+S”÷COF×ī“ó£»
Ź±£¬S”÷BEF+S”÷COF×ī“ó£»
¼“ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±”÷BEFÓė”÷COFµÄĆ껿֮ŗĶ×ī“óŹ±£¬AE=![]() £»¹Ź“ķĪó£»
£»¹Ź“ķĪó£»
£Ø5£©”ß”ĻEOG=”ĻBOE£¬”ĻOEG=”ĻOBE=45”ć£¬
”ą”÷OEG”×”÷OBE£¬
”ąOE£ŗOB=OG£ŗOE£¬
”ąOGOB=OE2£¬
”ßOB=![]() BD£¬OE=
BD£¬OE=![]() EF£¬
EF£¬
”ąOGBD=EF2£¬
”ßŌŚ”÷BEFÖŠ£¬EF2=BE2+BF2£¬
”ąEF2=AE2+CF2£¬
”ąOGBD=AE2+CF2£®¹ŹÕżČ·£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
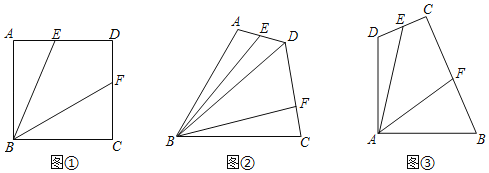
”¾ĢāÄæ”æ”÷ABCÖŠ£¬AB£½AC£¬”ĻABC£½¦Į£¬¹żµćA×÷Ö±ĻßMN£¬Ź¹MN”ĪBC£¬µćDŌŚÖ±ĻßMNÉĻ£¬×÷ÉäĻßBD£¬½«ÉäĻßBDČʵćBĖ³Ź±ÕėŠż×Ŗ½Ē¦Įŗó½»Ö±ĻßACÓŚµćE£®
£Ø1£©ČēĶ¼¢Ł£¬µ±¦Į£½60”ć£¬ĒŅµćDŌŚÉäĻßANÉĻŹ±£¬Ö±½ÓŠ“³öĻ߶ĪAB£¬AD£¬AEµÄŹżĮæ¹ŲĻµ£®
£Ø2£©ČēĶ¼¢Ś£¬µ±¦Į£½45”ć£¬ĒŅµćDŌŚÉäĻßANÉĻŹ±£¬Ö±Š“³öĻ߶ĪAB”¢AD”¢AEµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
£Ø3£©µ±¦Į£½30”揱£¬ČōµćDŌŚÉäĻßAMÉĻ£¬”ĻABE£½15”ć£¬AD£½![]() ©1£¬ĒėÖ±½ÓŠ“³öĻ߶ĪAEµÄ³¤¶Č£®
©1£¬ĒėÖ±½ÓŠ“³öĻ߶ĪAEµÄ³¤¶Č£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĢį³öĪŹĢā£ŗ£Ø1£©ČēĶ¼¢Ł£¬Õż·½ŠĪABCDÖŠ£¬µćE£¬µćF·Ö±šŌŚ±ßADŗĶ±ßCDÉĻ£¬ČōÕż·½ŠĪ±ß³¤ĪŖ4£¬DE+DF£½4£¬ŌņĖıߊĪBEDFµÄĆ껿ĪŖ”” £®
Ģ½¾æĪŹĢā£ŗ£Ø2£©ČēĶ¼¢Ś£¬ĖıߊĪABCD£¬AB£½BC£½4£¬”ĻABC£½60”ć£¬”ĻADC£½120”ć£¬µćE”¢F·Ö±šŹĒ±ßADŗĶ±ßDCÉĻµÄµć£¬Į¬½ÓBE£¬BF£¬ČōED+DF£½3£¬BD£½2![]() £¬ĒóĖıߊĪEBFDµÄĆ껿£»
£¬ĒóĖıߊĪEBFDµÄĆ껿£»
½ā¾öĪŹĢā£ŗ£Ø3£©Ä³µŲÖŹæ±Ģ½¶ÓĪŖĮĖ½ųŠŠ×ŹŌ“Öś²ā£¬½ØĮ¢ĮĖČēĶ¼¢ŪĖłŹ¾µÄŅ»øöĖıߊĪŅ°Ķāæ±²é»łµŲ£¬»łµŲĻąĮŚĮ½²ą±ß½ēDA”¢AB³¤¶Č¾łĪŖ4km£¬”ĻDAB£½90”ć£¬ÓÉÓŚæ±²āŠčŅŖ¼°¼¼ŹõŌŅņ£¬Ö÷æ±²āŅĒCÓė»łµŲ±ßŌµD”¢B¼Š½ĒĪŖ90”ć£Ø”ĻDCB£½90”ć£©£¬ŌŚ±ß½ēCDŗĶ±ß½ēBCÉĻ·Ö±šÓŠĮ½øöøØÖśæ±²āŅĒEŗĶF£¬øØÖśæ±²āŅĒEŗĶFÓėÖ÷æ±²āŅĒCµÄ¾ąĄėÖ®ŗĶŹ¼ÖÕµČÓŚ4km£ØCE+CF£½4£©£®ĪŖĮĖ“ļµ½øüŗĆ¼ą²āŠ§¹ū£¬Šč±£Ö¤æ±²āĒųÓņ£ØĖıߊĪEAFC£©Ć껿¾”æÉÄÜ“ó£®ĒėĪŹæ±²āĒųÓņĆ껿ӊƻӊ×ī“óÖµ£¬Čē¹ūÓŠĒó³ö×ī“óÖµ£¬Čē¹ūƻӊ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬AD”ĪBC£¬”ĻB£½90”ć£¬AB£½8£¬tan”ĻCAD£½![]() £¬CA£½CD£¬E”¢F·Ö±šŹĒAD”¢ACÉĻµÄ¶Æµć£ØµćEÓėA”¢D²»ÖŲŗĻ£©£¬ĒŅ”ĻFEC£½”ĻACB£®
£¬CA£½CD£¬E”¢F·Ö±šŹĒAD”¢ACÉĻµÄ¶Æµć£ØµćEÓėA”¢D²»ÖŲŗĻ£©£¬ĒŅ”ĻFEC£½”ĻACB£®
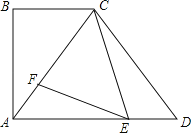
£Ø1£©ĒóCDµÄ³¤£»
£Ø2£©ČōAF£½2£¬ĒóDEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬ĻŅ![]() £¬
£¬![]() £¬
£¬![]() µÄĘ½·ÖĻß½»”ŃOÓŚµćD£¬Ēó£ŗ
µÄĘ½·ÖĻß½»”ŃOÓŚµćD£¬Ēó£ŗ
£Ø1£©BC£¬ADµÄ³¤£»
£Ø2£©Ķ¼ÖŠĮ½ŅõÓ°²æ·ÖĆ껿֮ŗĶ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涞“ĪŗÆŹży£½ax2£«bx£«cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬øł¾ŻĶ¼Ļó½ā“šĻĀĮŠĪŹĢā£ŗ
(1)Š“³ö·½³Ģax2£«bx£«c£½0µÄĮ½øöøł£»
(2)µ±xĪŖŗĪÖµŹ±£¬y£¾0£æµ±xĪŖŗĪÖµŹ±£¬y£¼0?
(3)Š“³öyĖęxµÄŌö“ó¶ų¼õŠ”µÄ×Ō±äĮæxµÄȔֵ·¶Ī§£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŗŠÖŠÓŠČōøÉƶŗŚĘåŗĶ°×Ę壬ÕāŠ©Ęå³żŃÕÉ«ĶāĪŽĘäĖū²ī±š£¬ĻÖČĆѧɜ½ųŠŠĆžĘåŹŌŃé£ŗĆæ“ĪĆž³öŅ»Ć¶Ę壬¼ĒĀ¼ŃÕÉ«ŗó·Å»ŲŅ”ŌČ£®ÖŲø“½ųŠŠÕāŃłµÄŹŌŃéµĆµ½ŅŌĻĀŹż¾Ż£ŗ
ĆžĘåµÄ“ĪŹżn | 100 | 200 | 300 | 500 | 800 | 1000 |
Ćžµ½ŗŚĘåµÄ“ĪŹżm | 24 | 51 | 76 | 124 | 201 | 250 |
Ćžµ½ŗŚĘåµÄʵĀŹ | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
£Ø1£©øł¾Ż±ķÖŠŹż¾Ż¹Ą¼Ę“ÓŗŠÖŠĆž³öŅ»Ć¶ĘåŹĒŗŚĘåµÄøÅĀŹŹĒ”” ””£»£Ø¾«Č·µ½0.01£©
£Ø2£©ČōŗŠÖŠŗŚĘåÓė°×Ęå¹²ÓŠ4ƶ£¬Ä³Ķ¬Ń§Ņ»“ĪĆž³öĮ½Ć¶Ę壬Ēė¼ĘĖćÕāĮ½Ć¶ĘåŃÕÉ«²»Ķ¬µÄøÅĀŹ£¬²¢ĖµĆ÷ĄķÓÉ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=©x2+bx+cÓėxÖį·Ö±š½»ÓŚµćA”¢B£¬ÓėyÖį½»ÓŚµćC£¬ĒŅOA=1£¬OB=3£¬¶„µćĪŖD£¬¶Ō³ĘÖį½»xÖįÓŚµćQ£®

£Ø1£©ĒóÅ×ĪļĻ߶ŌÓ¦µÄ¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©µćPŹĒÅ×ĪļĻߵĶŌ³ĘÖįÉĻŅ»µć£¬ŅŌµćPĪŖŌ²ŠÄµÄŌ²¾¹żA”¢BĮ½µć£¬ĒŅÓėÖ±ĻßCDĻąĒŠ£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚŅ»µćM£¬Ź¹µĆ”÷DCM”×”÷BQC£æČē¹ū“ęŌŚ£¬Ēó³öµćMµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚµČ±ß”÷ABCÖŠ£¬DĪŖBC±ßÉĻŅ»µć£¬EĪŖAC±ßÉĻŅ»µć£¬ĒŅ”ĻADB+”ĻEDC=120”ć£®
£Ø1£©ĒóÖ¤£ŗ”÷ABD”×”÷DCE£»
£Ø2£©ČōCD=12£¬CE=3£¬Ēó”÷ABCµÄÖܳ¤£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com