
 ���ϣ�һ��أ����������a��b���ɶ���ʽ�ij˷�������Եõ�
���ϣ�һ��أ����������a��b���ɶ���ʽ�ij˷�������Եõ� ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
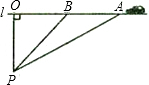 �ݽ��ܲ���ͳ�ƣ�������ʻ��������ͨ�¹ʵ���Ҫԭ��ijУ��ѧ����С��ļ���ͬѧ�볢�����Լ���ѧ��֪ʶ���٣�˫�����ij·�ε������ǣ�ÿСʱ80ǧ�ף������ʱ�ٲ�����80ǧ�ף�����ͼ�����ǽ��۲�����ڵ���·l�ľ���Ϊ0.1ǧ��P������ʱ��һ���γ��ɽ�����ɽ��»�ڻ�������ֱ��ʻ������ô˳���A����ʻ��B�����õ�ʱ��Ϊ3�룬����á�APO=59�㣬��BPO=45�㣮�Լ���AB���жϴ˳��Ƿ��٣����ο����ݣ�sin59���0.86��cos59���0.52��tan59���1.66��
�ݽ��ܲ���ͳ�ƣ�������ʻ��������ͨ�¹ʵ���Ҫԭ��ijУ��ѧ����С��ļ���ͬѧ�볢�����Լ���ѧ��֪ʶ���٣�˫�����ij·�ε������ǣ�ÿСʱ80ǧ�ף������ʱ�ٲ�����80ǧ�ף�����ͼ�����ǽ��۲�����ڵ���·l�ľ���Ϊ0.1ǧ��P������ʱ��һ���γ��ɽ�����ɽ��»�ڻ�������ֱ��ʻ������ô˳���A����ʻ��B�����õ�ʱ��Ϊ3�룬����á�APO=59�㣬��BPO=45�㣮�Լ���AB���жϴ˳��Ƿ��٣����ο����ݣ�sin59���0.86��cos59���0.52��tan59���1.66���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+x+6=0 | B�� | x2+x-6=0 | C�� | x2-x+6=0 | D�� | x2-x-6=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=1}\\{y=4.5}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 22015 | B�� | -22015 | C�� | -22014 | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{9x}$ | B�� | $\sqrt{3{x^2}}$ | C�� | $\sqrt{{x^2}-4}$ | D�� | $\sqrt{0.2x}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com