
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.

【答案】①②③④
【解析】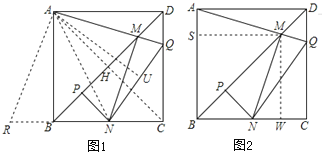
①如图1,作AU⊥NQ于U,交BD于H,连接AN,AC,
∵∠AMN=∠ABC=90°,
∴A,B,N,M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴AM=MN;
②由同角的余角相等知,∠HAM=∠PMN,
∴Rt△AHM≌Rt△MPN,
∴MP=AH=![]() AC=
AC=![]() BD;
BD;
③∵∠BAN+∠QAD=∠NAQ=45°,
∴在∠NAM作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,
∴△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ,BN=NU,DQ=UQ,
∴点U在NQ上,有BN+DQ=QU+UN=NQ;
④如图2,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,
∴四边形SMWB是正方形,有MS=MW=BS=BW,
∴△AMS≌△NMW
∴AS=NW,
∴AB+BN=SB+BW=2BW,
∵BW:BM=1: ![]() ,
,
∴![]() .
.
故答案为:①②③④


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 和
和![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求线段
,求线段![]() 的长;
的长;
(3)在![]() 的条件下,求
的条件下,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,运动到点
运动,运动到点![]() 即停止;同时点
即停止;同时点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,运动到点
运动,运动到点![]() 即停止.点
即停止.点![]() 、
、![]() 的速度的速度都是
的速度的速度都是![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,设点
,设点![]() 、
、![]() 运动的时间为
运动的时间为![]() .
.

![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 是矩形?
是矩形?
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形?
是菱形?
![]() 分别求出
分别求出![]() 中菱形
中菱形![]() 的周长和面积.
的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,有一抛物线
中,有一抛物线![]() ,与
,与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,现将背面完全相同,正面分别标有数
,现将背面完全相同,正面分别标有数![]() 、
、![]() 、
、![]() 、
、![]() 的
的![]() 张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点
张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点![]() 的横坐标,将该数的平方作为点
的横坐标,将该数的平方作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 落在抛物线与
落在抛物线与![]() 轴围成的区域内(含边界)的概率为________.
轴围成的区域内(含边界)的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点![]() ,
,![]() ,
,![]() 三点.
三点.

![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若点
若点![]() 是线段
是线段![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),过
重合),过![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
![]() 在
在![]() 的条件下,连接
的条件下,连接![]() ,
,![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 的面积最大?若存在,求
的面积最大?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京张高铁是世界上首条智能化高速铁路,起点是北京北,终点是张家口南.建成后的京张高铁铁路运行里程由原来的196km缩短为174km,运行时间缩短为原来的![]() ,平均速度比原来快150千米/小时.求建成后的京张高铁从北京北至张家口南的运行时间.
,平均速度比原来快150千米/小时.求建成后的京张高铁从北京北至张家口南的运行时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3![]() ,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )
,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )

A. 7 B. 8 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 边长为
边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() ,
,![]() 上当
上当![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在边
随之在边![]() 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD为边BC上的中线,点E在AD上,以点A为圆心,AB长为半径画弧,交BE的延长线于点F,点G在EF上,且∠EAG=∠CAF,连接CE.
(1)依题意补全图形;
(2)求证:FG=CE;
(3)若EF平分∠AEC,则∠BAE与∠ABE满足的等量关系为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com