
【题目】如图, ![]() 平分
平分 ![]() ,
, ![]() 于点
于点 ![]() ,
, ![]() ,点 P
,点 P![]() 从
从 ![]() 出发,以
出发,以 ![]() 的速度沿线段
的速度沿线段 ![]() 向终点
向终点 ![]() 运动;同时,点
运动;同时,点 ![]() 从
从 ![]() 出发,以
出发,以 ![]() 的速度沿射线
的速度沿射线 ![]() 运动,当点 P到达终点
运动,当点 P到达终点 ![]() 时,则两点均停止运动. 那么经过
时,则两点均停止运动. 那么经过 ![]() ,能使
,能使 ![]() .
.
【答案】![]() 或
或 ![]()
![]()
【解析】解:(1)当P、Q移动到如图1所示位置时,过点A作AC![]() OM于点C,
OM于点C,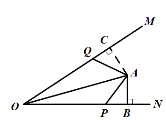
图1
设经过x秒时,AP=AQ,此时BP=x,OP=6-x,OQ=3x,
∵O A 平分 ∠ M O N ,∴AC=AB,又∵AP=AQ,∴![]() ACQ
ACQ![]()
![]() ABP,∴CQ=BP,
ABP,∴CQ=BP,
∵∠AOC=∠AOB,∠ACO=∠ABO,OA=OA,∴![]() ACO
ACO![]()
![]() ABO,∴CO=BO,
ABO,∴CO=BO,
∴CO-CQ=BO-BP,即OQ=OP,即:6-x=3x,解得:x=1.5.
(2)当P、Q移动到如图2所示位置时,过点A作AC![]() OM于点C,
OM于点C,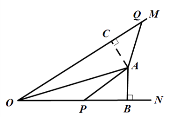
图2
设经过y秒时,AP=AQ,此时BP=y,OP=6-y,OQ=3y,
由(1)可得![]() ACQ
ACQ![]()
![]() ABP,∴CQ=BP=y,
ABP,∴CQ=BP=y,
由(1)可得![]() ACO
ACO![]()
![]() ABO,∴CO=BO,
ABO,∴CO=BO,
即:OQ-CQ=BO,即3y-y=6,解得:y=3.
(3)当点 P在(2)的基础上继续移动,到达终点 O 时,此过程无AP=AQ的情形.
所以答案是:1.5或3.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只小球落在数轴上的某点![]() ,第一次从
,第一次从![]() 向左跳1个单位到
向左跳1个单位到![]() ,第二次从
,第二次从![]() 向右跳2个单位到
向右跳2个单位到![]() ,第三次从
,第三次从![]() 向左跳3个单位到
向左跳3个单位到![]() ,第四次从
,第四次从![]() 向右跳4个单位到
向右跳4个单位到![]() ……若按以上规律跳了6次时,它落在数轴上的点
……若按以上规律跳了6次时,它落在数轴上的点![]() 所表示的数恰好是2017,则这只小球的初始位置点
所表示的数恰好是2017,则这只小球的初始位置点![]() 所表示的数是_______,若按以上规律跳了2n次时,它落在数轴上的点
所表示的数是_______,若按以上规律跳了2n次时,它落在数轴上的点![]() 所表示的数恰好是a,则这只小球的初始位置点
所表示的数恰好是a,则这只小球的初始位置点![]() 所表示的数是________.
所表示的数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将正比例函数y=kx(k>0)的图象向上平移一个单位,那么平移后的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com