
 已知:D是等边△ABC中BC边上一个不与B,C重合的动点,且△ADE也是等边三角形.
已知:D是等边△ABC中BC边上一个不与B,C重合的动点,且△ADE也是等边三角形.分析 (1)根据等边三角形的性质得到∠B=∠C=∠3=60°,于是得到∠1+∠2=∠DFC+∠2,推出△ABD∽△DCF;由于∠E=∠C=60°,∠AFE=∠DFC,得到△AFE∽△DCF,根据相似三角形的传递性得到△AFE∽△ABD,即可得到结论;
(2)连接CE,根据等边三角形的性质得到AB=AC,AD=AE,∠B=∠ACB=60°,∠BAC=∠DAE=60°,推出△BAD≌△CAE(SAS),得到BD=CE,过D作DH⊥AB于H,解直角三角形即可得到结论;
(3)根据已知条件△AEF与△FDC面积的差为$\sqrt{3}$,于是得到△ADE与△ADC的面积差=$\sqrt{3}$,根据三角形的面积公式得到$\frac{\sqrt{3}}{4}$(AD2-AB2+AB•BD)=$\sqrt{3}$,在Rt△ADH中,根据勾股定理得到BD2=AD2-AB2+AB•BD,②,化简整理即可得到结论.
解答  (1)证明:∵△ABC,△ADE为等边三角形,
(1)证明:∵△ABC,△ADE为等边三角形,
∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,
∴∠1=∠DFC,
∴△ABD∽△DCF;
∵∠E=∠C=60°,∠AFE=∠DFC,
∴△AFE∽△DCF,
∴△AFE∽△ABD,
∴与△ABD相似的三角形一共有2个,它们是△AEF与△CDF;
故答案为:2,△AEF与△CDF;
(2)解:连接CE,
∵△ABC为等边三角形,△ADE也是等边三角形,
∴AB=AC,AD=AE,∠B=∠ACB=60°,∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴BD=CE,
过D作DH⊥AB于H,
∵∠B=60°,BD=CE=2$\sqrt{3}$,∴BH=$\frac{1}{2}$BD=$\sqrt{3}$,DH=3,
∴AH=8,AD=$\sqrt{A{H}^{2}+D{H}^{2}}$=$\sqrt{73}$,
∴△ADE的边长是$\sqrt{73}$;
(3)解:∵△AEF与△FDC面积的差为$\sqrt{3}$,
∴△ADE与△ADC的面积差=$\sqrt{3}$,
∴S△ADE-(S△ABC-S△ABD)=$\frac{1}{2}$•AD2sin60°-$\frac{1}{2}$•AB2sin60°+$\frac{1}{2}$AB•BDsin60°
=$\frac{\sqrt{3}}{4}$(AD2-AB2+AB•BD)=$\sqrt{3}$,①,
在Rt△ADH中,∵AD2=AH2+DH2,
∵BH=$\frac{1}{2}$BD,DH=$\frac{\sqrt{3}}{2}$BD,
∴AD2=(AB-$\frac{1}{2}$BD)2+($\frac{\sqrt{3}}{2}$BD)2,
=AB2-AB•BD+BD2,
∴BD2=AD2-AB2+AB•BD,②,
把②代入①得:$\frac{\sqrt{3}}{4}$BD2=$\sqrt{3}$,
∴BD=2.
点评 此题主要考查了相似三角形的判定方法,等边三角形的性质等知识,全等三角形的判定和性质,得出对应角关系是解题关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
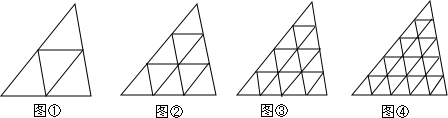
| 等分数n | 小三角形个数a | 顶点数b | 边数c |
| 2 | 4 | 6 | 9 |
| 3 | 9 | 10 | 18 |
| 4 | 16 | 15 | 30 |
| 5 | 25 | 21 | 45 |
| … | … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
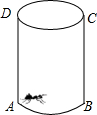 如图所示的圆柱体中底面圆的半径是$\frac{3}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是3$\sqrt{2}$(结果保留根号).
如图所示的圆柱体中底面圆的半径是$\frac{3}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是3$\sqrt{2}$(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | ±$\frac{1}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE:AD=2:3,CD=3cm,则AF的长为( )
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE:AD=2:3,CD=3cm,则AF的长为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com