
【题目】在东西向的马路上有一个巡岗亭![]() ,巡岗员从岗亭
,巡岗员从岗亭![]() 出发以
出发以![]() 速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)第几次结束时巡逻员甲距离岗亭![]() 最远?距离
最远?距离![]() 有多远?
有多远?
(2)甲巡逻过程中配置无线对讲机,并一直与留守在岗亭![]() 的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
科目:初中数学 来源: 题型:
【题目】如图, DE AB 于 E , DF AC 于 F ,若 BD CD 、 BE CF ,
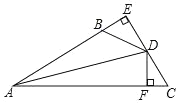
(1)求证:AD平分BAC ;
(2)已知AC 14,BE 2,求AB的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.
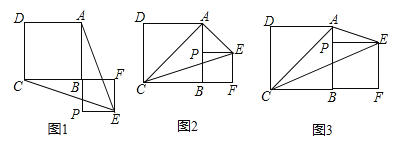
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 中的点
中的点![]() 是
是![]() 边上的一点,过点
边上的一点,过点![]() 的反比例函数
的反比例函数![]()
![]() 与
与![]() 边交于点
边交于点![]() ,连接
,连接![]() .
.
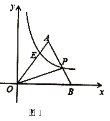
(1)如图1,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的面积为5,求直线
的面积为5,求直线![]() 和反比例函数
和反比例函数![]() 的解析式;
的解析式;
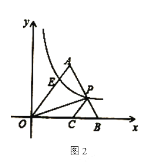
(2)如图2,若![]() ,过
,过![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() ,并且
,并且![]() 的面积为
的面积为![]() ,求反比例函数
,求反比例函数![]() 的解析式及点
的解析式及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段PQ=1,点P1是线段PQ的中点,点P2是线段P1Q的中点,点P3是线段P2Q的中点..以此类推,点pn是线段pn1Q的中点.
(1)线段P3Q的长为 ;
(2)线段pnQ的长为 ;
(3)求PP1+P1P2+P2P3+…+P9P10的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D在BC边上,把△ABD沿AD折叠后,使得点B落在点E处,连接CE,若∠DBE=20°,则∠ADC=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .对于下列结论:
.对于下列结论:
①![]() ;②
;②![]() ;③
;③![]() .其中正确的是( )
.其中正确的是( )
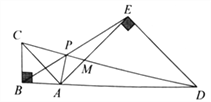
A. ①②③ B. ① C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
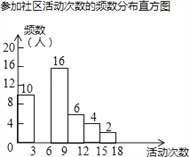
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | m | b |
15<x≤18 | 2 | n |
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com